What Goes Around
 
Version 1.2
Copyright ©2017 by Paul Niquette. All rights reserved.


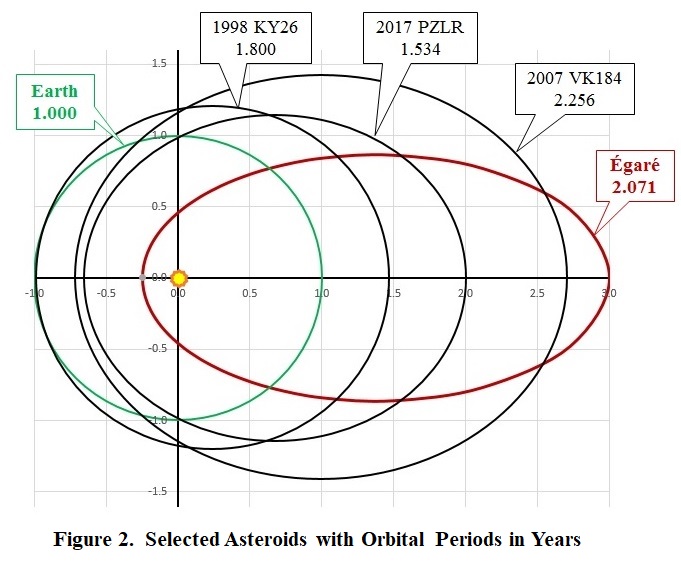
Reprised from the puzzle, the sketch in Figure 2 depicts four asteroid orbits, along with their respective orbital periods.  Solvers have been asked...

What is your Prediction for the period of time between intervals
during which each asteroid threatens to collide with Earth?


orbper1

The question was answered in the puzzle for Égaré by using ф = 7.138 minutes to quantize time, inasmuch as that is the interval during which our planet is capable of blocking an asteroid at an orbital intersection.  And our answer was 76,300 years for both intersections.

Using the same assumptions, we have these answers for the What Goes Around puzzle...

Égaré ~~~~~~~~~~~~~ 76,300 years
1998 KY26 ~~~~~~~~~~~~ 83,116 years
2007 VK184 ~~~~~~ 66,316 years
2017 PZLR ~~~~~ 56,516 years

...however, one assumption was not made explicit -- that the quantizing interval ф = 7.138 minutes for EarthEarthEarthEarth's year should be the same at all orbital intersections regardless of the angle at which the near-coplanar asteriod approaches.  That seems quite doubtful. 
Consider the asteroid 1998 KY26, which has a near-osculating orbit with that of Earth.  Whereas the duration of a cross-over event is elongated, the time between cross-over events stays the same, whatever the quantizing interval ф.

Another consideration is orbital resonance.  Suppose that by happenstance the orbital period for Égaré τ =  730.500 days instead of x ad756.433 days.  Since 730.500 = τ =  τ =  2.000 x 365.25, Égaré would be in 2:1 resonance with Earth.  Although the orbits will intersect, there will be no collisions.  In effect the time between threats becomes infinite.

Same for any ratios of integers representing orbital periods.  Well, let's make that for "any  ratios of small integers."  The integers 2,071 and 1,000 are not small, and their ratio brings us back to our 76,300 years between collision threats by Égaré.
Imagine a long-period comet sweeping in from beyond Jupiter to cross Earth's orbit.  Astronomers have determined that the comet has an extremely eccentric orbit with a period measured in centuries.  Scrambling to ascertain the comet's orbital parameters, they report that the perihelion is less than 1AU and, most alarmingly, its orbital inclination is less than one degree!   With just that information, might a solver of the What Goes Around puzzle provide a preliminary estimate for the probability of collision?
At the instant the comet arrives at an intersection, which is not yet determined, Earth will be occupying some point on its orbit for ф = 7.138 minutes.  There are  365.250 x 24 x 60 /7.138 minutes 7.138 = 525,960525,960525,960 such locations. Since the comet constitutes a coplanar threat, exactly two of those locations will coincide with orbital intersections.  So the probability of collision is about 1 chance in 250,000.7.138 minutes
ré
Sophisticated solvers will take notice that one of the orbits the sketch in Figure 2the sketch in Figure 2depicted in Figure 2 meets the conditions in the solution to the Astrogating Asteroids puzzle, such that the two orbital intersections are the same for any inclination.  Nevertheless, that does not put in doubt the solution in the Orbital Deflection puzzle -- even for asteroid 2017 PLZR.  Why is that?

ifilmiAsteroid Hazards: The View from Space, Part 2
           The Challenge of Detection
Thomas Statler, Astrophysicist & Planetary Scientist

Nota bene, the assumption for all asteroids in the What Goes Around puzzle have orbits that are simple solutions to Kepler's Laws of Planetary Motion -- that each is acted upon by the gravitational force of the sun and no other celestial body.  Solvers will discover some interesting realities about orbital Predictions in the Plural Gravities puzzle.

Solvers, your comments are invited.

 
Home Page
Puzzle Page
Space Stuff
 Puzzle as a Literary Genre