|
What goes around comes around Version 1.1 Copyright ©2017 by Paul Niquette. All rights reserved. |
|||
ORBITAL
METAL: BILLY MOON
Metal Wall Art: sculpture, hand forged iron loops finished in lightly burnished silver leaf.
1.
Detection of threats
from NEOs based on their sizes and
orbital parameters. 2.
Prediction of the orbital
motion of each NEO to ascertain its
likely point of impact. 3.
Deflection of the
threatening NEO's orbit to avoid
collision with Planet Earth.
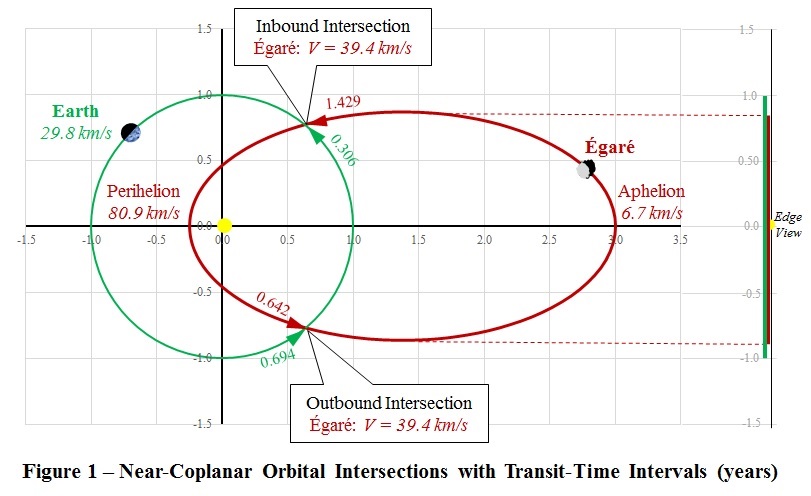
In the Rock from the Sky puzzle, solvers were warned that Égaré had been predicted to arrive at the inbound orbital intersection on the same day as planet Earth passes the same point in its orbit -- that day being Thursday, July 21, 2022. The Prediction was regarded to be quite worrisome, and the Orbital Deflection puzzle invited solvers to invent a way to change the inclination of the asteroid's orbit to prevent its collision with our planet. On that day, though, Earth may arrive several hours after Égaré has gone by. Then too, with only the date given in the Prediction, solvers need not be surprised if the asteroid passes behind the earth by, say, a half-day’s time. Inasmuch as the Earth is a ‘moving target’, to determine the probability of a collision on Thursday, July 21, 2022, one must estimate how many of those 24-hours Earth will spend blocking the path of Égaré… With an orbital radius of 150 Mkm, our planet travels through space 942.5 Mkm every year. That's 2.6 Mkm each day or 107,600 km/h. Earth's diameter at the Equator is about 12,800 km. Thus, planet Earth requires only 7 minutes and 8 seconds to pass across any point on its orbit. That’s less than 1/200th of a day.
For 365.250 m = 756.433 n, we have that m = 756.433 and n = 365.250. The common products 365.250 x 756.433 = 276,287.153 days or about 756 years.Both Earth and Égaré will arrive at the inbound intersection of their orbits on the same day about 756 years after 2022 or in the year 2778. Similarly, both celestial bodies will meet at the outbound intersection of their orbits every 756 years, so potential collision days will occur twice per 756 years or about once every 378 years. On each of those joint arrival days, the probability of impact is about 1/200. We might want to combine the day-of-intersecting and the probability-of-colliding during that day... Instead of using 24-hour days, let’s quantize the planet Earth's year by a unit of time ф = 7.138 minutes, which is the time required for our planet to move along its orbit a distance equal to its diameter at the equator.Well then, one year on Earth = 73,684.505 ф. The orbital period for Égaré τ = 2.071 x 73,684.505 = 152,600.611 ф. The common products 73,684.505 x 152,600.611 = 11,244,300,484.200 ф or 152,601 years, or 76,300 years considering both intersections. Apparently, we can estimate the interval between impact threats by simply deriving a quantizing unit ф based on the cross-section-in-time of planet Earth During the preparation of the What Goes Around puzzle, a headlined appeared: Small Asteroid Gives Earth a Close Shave in Highly Anticipated Flyby.Perhaps the quantizing unit ф should be increased for the Prediction of collisions with geostationary satellites. Thus, for ф = 10.244 minutes, the interval between threats by Égaré is reduced from 76,300 to 53,032 years.
...along with two fictitious asteroids, Égaré and Puzzler. The latter was studied in the Astrogating Asteroids puzzle. For simplicity in comparisons, all four orbits have their major axes rotated to be horizontal in the sketch. 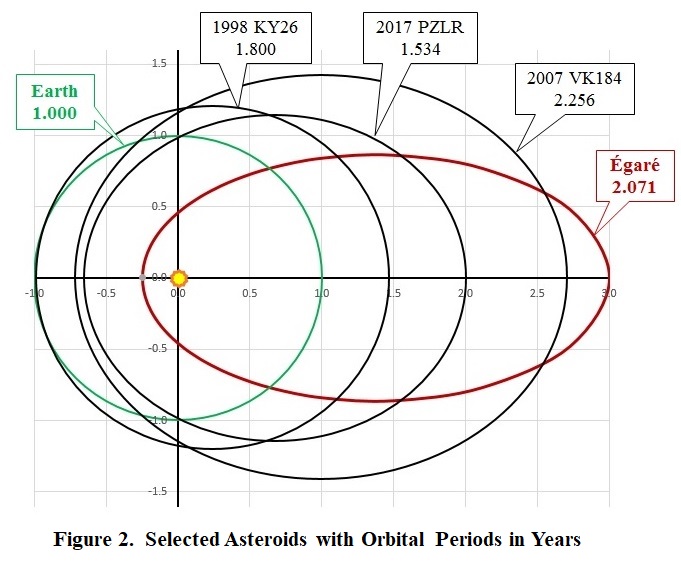
 |

 Asteroid
Hazards: The View from Space, Part 3
Asteroid
Hazards: The View from Space, Part 3