 Copyright ©2010 by Paul Niquette. All rights reserved. |
|
 Solvers
of Green Flight will be
well acquainted with aerodynamic drag,
specifically that there are two kinds, "parasitic drag"
and "induced drag." For our purposes here, it will
be useful to regard the latter as resulting from the
"Need for speed," as explored in other puzzles,
including Look-at-Me Car
and Steamboat Hill.
The latter form -- parasite drag -- is more properly
named "lift induced drag." It is a
consequence unique to things that fly, and we have
dubbed it Wages of Flight.
We seek a simple relationship between fuel consumption rate F (gph) and airspeed V (mph), beginning with these symbols... D = aerodynamic drag (lbs)One might readily appropriate a conventional equation for Induced drag while applying the so-called Drag equation for parasite drag and thus write the sum... D = dP + dI = a" V 2 + b" / V 2...reminding ourselves that parasite drag increases as the square of airspeed while induced drag decreases with the square of airspeed. As many as a dozen technical factors and coefficients can be found embedded in that expression. Conversion parameter a" has the units lbs/(mph)2 and varies somewhat with altitude and outside air temperature. Conversion parameter b" has the units lbs-(mph)2 and varies with the square of lift, and lift is equal to aircraft weight. Since aircraft weight can only decrease during flight, using gross take-off weight in our calculation will assure a conservative approximation of drag. All other aircraft parameters, such as aircraft size and shape, do not change in flight, so we shall consider both a" and b" to be constant in level flight. As seen in the solution to Green Flight requisite horsepower H is proportional to both airspeed V and thrust, the latter being equal to drag D, so we write... H = D V = (a" V 2 + b" / V 2 ) V = a" V 3 + b" / V...in which we may substitute conversion parameters a' and b' and write... H = a' V 3 + b' / V...wherein a' has the units hp/(mph)3 and b' has the units hp-mph.
F = a V 3 + b / V...wherein a has the units gph/(mph)3 and b has the units gph-mph. With an assumed specific fuel consumption (lb/(hp·hr) for the aircraft's engines, both a and b may be considered as constants. Our object now is to ascertain the numerical values of a and b for Amelia Earhart's Lockheed Electra 10E. For that, two sets of corresponding values of F and V will give us two parametric equations in two unknowns. Here they are...
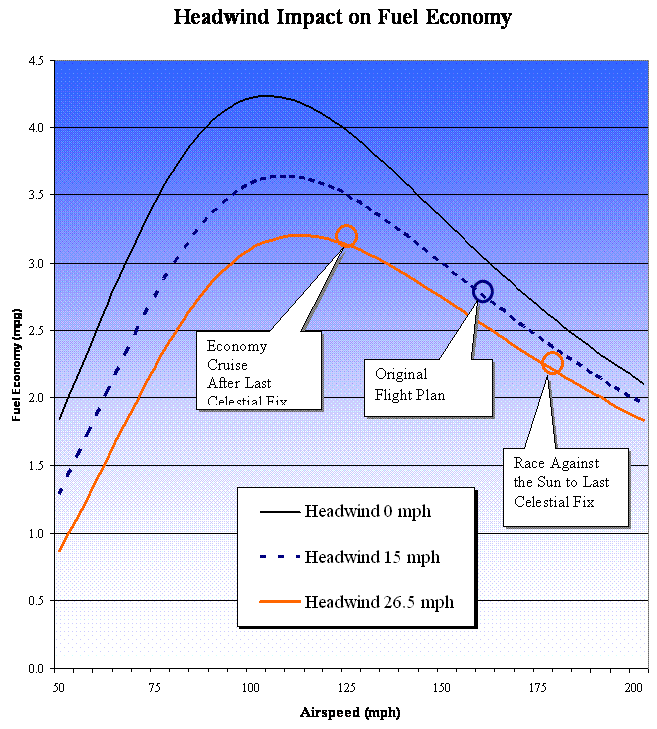
b = 1.29 (103) gph-mph, such that... F = 10.8 (10-6) V 3 + 1.29 (103) / V 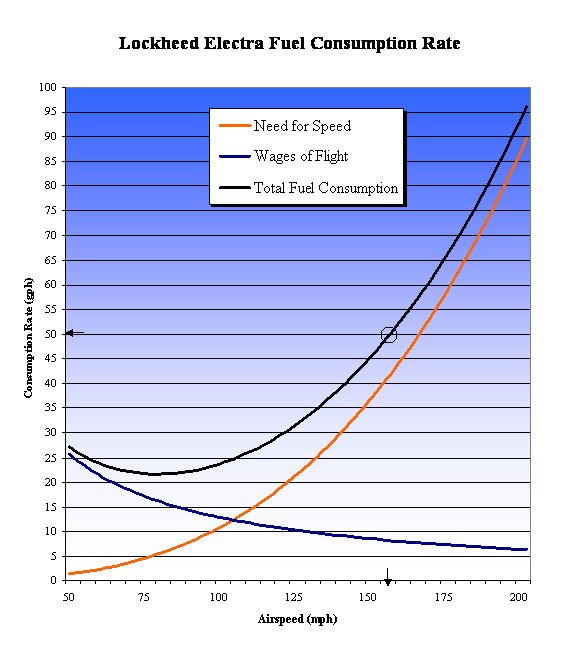 The estimated headwind of 15 mph is not indicated in this graph. The resulting ground speed of 142 mph means that, consuming 50.0 gph, the Electra would be getting 2.8 mpg. To make good the 2,556 miles from Lae to Howland would require a total of 18 hours of fuel or 900 gallons, leaving about 200 gallons in reserve. It is reasonable to assume that, upon arrival in the vicinity of Howland, the Electra would be throttled back to save fuel. At an airspeed of 100 mph, say, the engines would be consuming 23 gph according to the graph, and the 200 gallons in reserve would last for more than 8.5 hours. Reality #1: Amelia Earhart and Fred Noonan faced higher headwinds.Over the island of Nukumanu, some 850 miles from Lae, the Amelia Earhart reported a headwind of 26.5 mph. If we assume... {a} that wind speed to have prevailed for the whole 2,556 miles and...the flight's ground speed would have been reduced to 130.5 mph, and it would require 19.5 hours to reach Howland. With an airspeed of 157 mph facing a 26.5 mph headwind, the Electra would be getting 2.6 mpg. To make good the 2,556 miles would require a total of 983 gallons. But that still leaves nearly 117 gallons. With the Electra slowed to 100 mph., 117 gallons would last more than 5 hours. Reality #2: Amelia Earhart and Fred Noonan faced a deadline.Solvers of the Here Comes the Sun puzzle will be acutely aware that the rising sun would set a deadline for taking the last celestial fix. Furthermore, at some point in the flight, Fred Noonan must have become concerned about whether the radio direction finding would be functional for homing to Howland Island, as seen in the solution to Live Reckoning. His original plan for the last celestial fix was apparently intended to occur no more than 200 miles away from Howland, a point that would be reached at about 16:30 GCT on the original flight plan facing the estimated 15 mph headwind. To make good the original 142.0 mph ground speed facing the 26.5 mph headwind, would require an airspeed increase to 168.5 mph. Let this be our solution for Wages of Flight..
Accordingly, at
1,000 feet, a reasonable assumption for the headwind
would be 15 mph as originally estimated in Fred
Noonan's flight plan. The resulting
groundspeed flying at the economical 120 mph would
then be 105 mph for the last 250 miles to the
157-337 LOP, saving about 20 minutes. Given
all the conditions known to solvers...
Ironically, insofar as fuel consumption is concerned, it would have been more advisable for Amelia Earhart to set her cruise speed slower than the median 168.5 mph (165 mph, say) and thus more economical. Fred Noonan would then be required to take the last celestial fix farther from Howland resulting in larger navigation errors, as shown in the solution to the Live Reckoning puzzle and summarized in the solution to Which way, Amelia? |
