Pictured in our Trip Time puzzle is a "Baby Bullet" train operated by Caltrain as an SRO commuter-rail service in San Francisco.   For this analysis, let us use New York City Transit trains to illustrate a typical full-metro service.

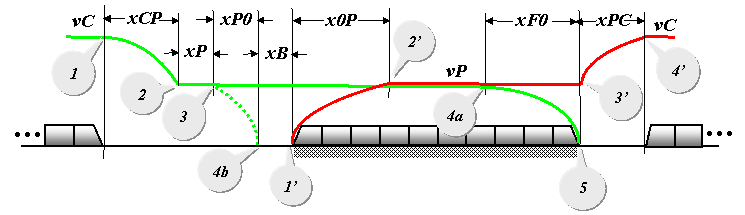If the platform is not occupied, the train operator sees a green light, which allows continuation at vP into the platform all the way to Point 4a where the operator performs a feathered stop at Point 5.

Stopped in the station platform, a train waits out its dwell time tD, during which doors are opened for unloading and loading of passengers.  Typically 20 seconds in duration, tD must be added directly to the Trip Time.

We now shift our attention to Point 1', the location of the rear-most extreme of the same train, with its phase-plane depicted in red in the sketch above.  When tD has elapsed, the conductor closes the doors and the operator commands the train to depart the station.  The train accelerates at a constant rate aS to vP, the platform operating speed, at Point 2'.

As the tail car reaches the far end of the platform at Point 3', the train is released to continue accelerating at aS from vP to cruise speed vC, which occurs well clear of the platform at Point 4'.

Here is a Base Case, using typical values...

• Train Length:  xL = 510 ft (10-car consist of R142 vehicles, each 51 ft long)
• Cruise Velocity: vC = 50 mph (73.3 fps)
• Platform Velocity: vP = 30 mph (44.0 fps)
• Normal Acceleration: aS = 2.5 mphps (3.7 fpsps)
• Service Braking Deceleration: dS = 3.0 mphps (4.4 fpsps)
• Feathered Stop Decleration: dF = 1.5 mphps (2.2 fpsps)
• Dwell Time: tD = 20 seconds

tSS = tCP + tP + (xPO / vP) + tB + (xL - xF0) / vP + tF0 + tD + t0P + (xL - x0P) / vP + tPC

...and during that time, the lead car of the train will have traveled a total distance of...

xSS = xCP + xP + xP0 + xB + xL + xPC + xL

If the station in the Base Case were bypassed, say, by an express train, that distance xSS would have been covered at cruise speed vC, such that tBYPASS = xSS / vC.  Thus, the difference in Trip Time tDELTA enjoyed by an express train in bypassing a local station can be calculated as follows:

tDELTA = tSS - tBYPASS.

Perturbations of the Base Case show some interesting interactions, if not ironic trade-offs...

1. Increasing acceleration and decelerations aS, dS, and dF by 10% improves tSS by about 4 seconds at every station and reduces the benefit of express service tDELTA by 2 seconds for each bypassed station.
2. Reducing buffer distances xP and xB by 10% will have neglible effects on tSS and tDELTA.
3. Overcrowding on a station platform can result in extending dwell time tD by some time we shall call tCRUSH, which will be added directly to both tSS and tDELTA.
4. Having both express and local services, an express station will likely reduce tCRUSH.  However, the same benefit would accrue to all stations by running more trains with closer headways.
5. Maximum cruise speed vC for R142 vehicles is 55 mph, 10% over the Base Case value.  That would make an improvement in the benefits of express service tDELTA by 3.5 seconds while penalizing station stops by 4.1 seconds!  You may regard the exclamation point as signifying a counter-intuitive consequence.