|
Copyright ©2010 by Paul Niquette. All rights reserved. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
 As
postulated in the puzzle, if
the California High Speed Rail (CHSR) project were to
adopt the World's Fastest Train
for the route from Sacramento to Los Angeles, a non-stop
service for the whole 412 miles would be covered in
about 1:09, assuming its record-setting speed... As
postulated in the puzzle, if
the California High Speed Rail (CHSR) project were to
adopt the World's Fastest Train
for the route from Sacramento to Los Angeles, a non-stop
service for the whole 412 miles would be covered in
about 1:09, assuming its record-setting speed...
#1. Maximum Train Velocity ~~~~~~~~~~~~~~~~~~~~~~~~~~~~ vMAX = 357 mph...but stopping at a station along the route will call for adding at least... #7. Station Dwell Time ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ tDWELL = 5 minutes...so that for a one-station stop, the time enroute increases to 1:14, which reduces the overall train speed to 333 mph. That matches the corresponding entry in the table for Solution {a}. Adding stops at all eight stations would increase the overall time enroute by 40 minutes to 1:49 and reduce the speed enroute to about 227 mph, which also matches the correspond entry for Solution {a}. Most solvers will notice that the entries in Solution {a} do not take into account braking time going into each intermediate station and the acceleration time following the dwell time. Those intervals can be calculated using... #5. Maximum Acceleration ~~~~~~~~~~~~~~~~~~~~~ aMAX = 0.1 g = 2.2 mphps...both being limited by passenger comfort. For each intermediate stop we might calculate as follows: Acceleration Time = vMAX / aMAX = 357 mph / 2.2 mphps = 162 sec = 2.7 minutes...and adding their absoute magnitudes (|2.7| = |-2.7|) to tDWELL gives us a total of about 10.4 minutes, resulting in a speed for the route of 310 mph. That matches the entry for Solution {b}. Checking the entry for eight enroute stations, we find an added time of 8 * 10.4 minutes or 1:23 for a total of 2:32 for the whole 412 miles at an average speed of 162 mph as offered in Solution {b}. Solvers of the Express vs Local puzzle will see something amiss in Solution {b}. All during deceleration and acceleration, the train is actually moving some distance along the trackway toward the destination. That distance is given by a familiar formula.. (vMAX)2 / aMAX = (357 * 5280/3600 fps)2 / (2.2 * 5280/3600 fpsps) = 85,000 ft...which amounts to 16 miles, with the station located at about the halfway point. If the World's Fastest Train bypassed that station, it would cover the 16 miles a whole lot faster than a train that is stopping at the station -- but not in zero time -- as apparently assumed in Solutions {a} and {b}. At 357 mph, the V150 takes 2.7 minutes to cover 16 miles, which should be deducted from the 10.4-minute time penalty for stopping at each station, giving a better estimate of 7.7 minutes per station. The average speed with one enroute station stop is given by 412 / 357 + 7.7 / 60 = 1.28 hours for an average speed of 321 mph, which matches the first entry in Solution {c}; Likewise for eight stops 412 / 357 + 8 * 7.7 / 60 = 1.28 hrs and 189 mph. However, as we shall see, Solutions
{a}, {b}, and {c} are all incorrect.
#3. Maximum Tractive Effort ~~~~~~~~~~~~~~~~~~~ eMAX = 27,600 pounds-forceOperating near the upper limit of its speed, the V150 will be facing its maximum in aerodynamic drag and using all of its... #2. Maximum Propulsive Power ~~~~~~~~~~~~~~~~~~ pMAX = 26,300 horsepower...to do so, with almost no power left over for acceleration. Solvers can easily confirm that by reviewing the video. As the train approaches 574.8 kph (357.0 mph), the acceleration has noticeable slowed to less than 1.0 kph/sec (0.6 mphps or about 1/100th of a g). When the train is pulling out of a station, nearly all of that 26,300 hp would be available for acceleration. And the V150 with... #4. Maximum Train Weight ~~~~~~~~~~~ wMAX = 100 tons = 200,000 pounds-force...could theoretically accelerate at eMAX/ wMAX = 27,600 / 200,000 = 0.14 g or 3.1 mphps. That would be excessive for passengers who are not strapped into their seats, as mandated for airliners. People of all ages may be standing or walking in the aisles or sipping coffee. It is customary to set a limit on accelerations to aMAX = 0.1 g or about 2.2 mphps. The graph below gives a normalized depiction in the time domain of acceleration and speeds on a V150 class train. 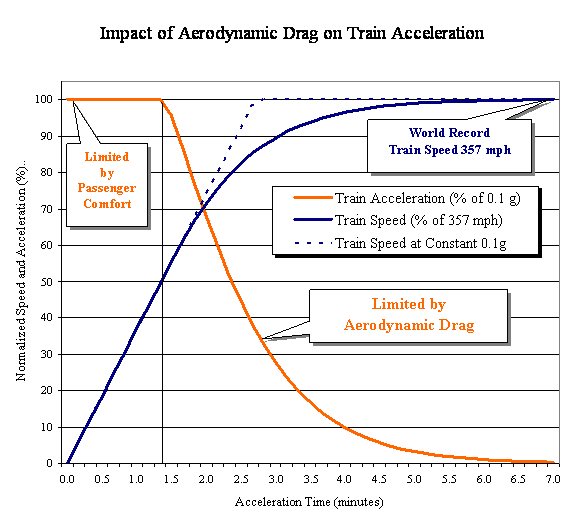 With constant acceleration aMAX, the V150's speed would increase linearly along the dashed line toward vMAX in about 3 minutes, as assumed in Solutions {a}, {b}, and {c}.Reality is something else. Aerodynamic drag increases according as the square of train-speed, and the required horsepower to overcome aerodynamic drag increases with the cube of train-speed. No matter how much of the V150's power is devoted to tractive effort eMAX, with increasing speed, more and more of that tractive effort is devoted to overcoming aerodynamic drag and thus unavailable for acceleration. Some solvers may notice that at a speed below about 180 mph (50% of the 357 mph) aerodynamic drag has not taken effect to reduce the acceleration below aMAX. The numbers suggest that any train with aerodynamic properties comparable to the V150's will show the same pattern. Since the present TGVs and Aerostars operate with a vMAX < 200 mph, the linear acceleration model applies to them. Exclamation Point Alert: At speeds faster than about 180 mph, all of the V150's 32 drive wheels will be on the brink of losing their frictional grip on the rails!
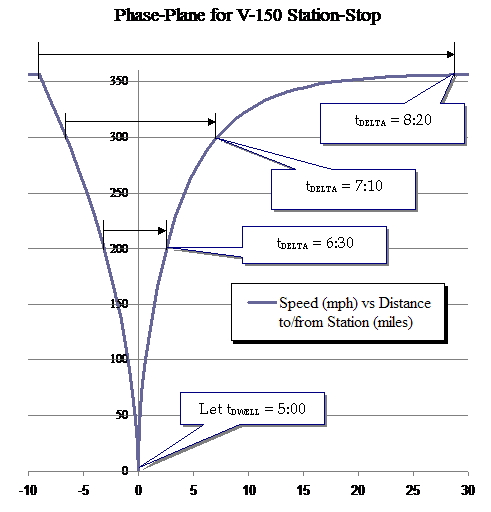
Thus, for the V150, tDELTA = 14.4 - 6.0 = 8.4 minutes. That 8.4 minutes is the estimated allowance in the timetable required for each intermediate station and is the basis for Solution {d}...
The model assumes a fixed value for tDWELL = 5 minutes, which is much longer than the typical value of tDWELL = 20 seconds used in full metro services for daily commuters on short segments. By way of justification, each duplex vehicle in the V150 consist is equipped with only one stairway and only one door at the platform level. In contrast, BART vehicles offer more than twice the number of doors per commuting passenger than do TGV train-sets for the cross-country travelers. Moreover, high-speed trains going long distances between stations require more time for loading and unloading passengers, since many are required to lug -- well, luggage. Finally, extra time embedded in tDWELL assures "feathered stopping" and reduction of "starting jerk." Superimposed on the phase-plane plot above are tDELTA values for hypothetical trains operating at lower vMAX than the World's Fastest Train. Solvers of the Express vs Local puzzle will not be surprised that tDELTA increases with vMAX along with tDWELL . One might ask, Does the increase in vMAX overcome the potential impact of tDELTA on trip-time? Yes, and then some (but not much).
 Back
to
the planned California
High
Speed Rail project with its eight intermediate
stations on the 412-mile route between Sacramento and
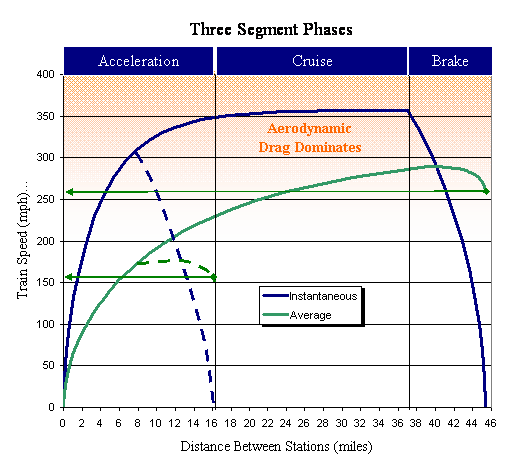
Los Angeles: As mentioned in the puzzle,
the segment distances range from 13 miles to 113 miles
and average 46 miles (412 / 9). By happenstance of
puzzle-making, that average fits the case in the graph
above and would allow the World's
Fastest Train to cruise at its world-record
speed of 357 mph between stations -- but for no more
than 48 seconds, on average Exclamation point
optional. Back
to
the planned California
High
Speed Rail project with its eight intermediate
stations on the 412-mile route between Sacramento and
Los Angeles: As mentioned in the puzzle,
the segment distances range from 13 miles to 113 miles
and average 46 miles (412 / 9). By happenstance of
puzzle-making, that average fits the case in the graph
above and would allow the World's
Fastest Train to cruise at its world-record
speed of 357 mph between stations -- but for no more
than 48 seconds, on average Exclamation point
optional. Epilog
Solvers
may notice several
references to the AGV's pantograph, which confirms
discoveries made in another
puzzle entitle Pantograph Design,
Meanwhile,
the residence of your puzzle-master is
now a mere 20 minutes away from
the station in Lamballe, which
will soon offer non-stop AGV
service to and from Paris at 300 km/hr (200
mph). Hoo-hah.
|