 We
discovered in the Station-Stop
puzzle
that cruise speed vC does not
play a part in determining
minimum headway tH. The Trip
Time puzzle was a
different matter.
There we ascertained the time between stations tS,
noting
that if the distance between stations xS
is large, as with
long-haul railroad services,
tS will approach xS /
vC.
Passenger transit systems, especially in urban
environments, will typically
require xS to be less than a couple of
miles, which brings into consideration
parameters other than vC for calculating
Trip
Time. Here is a Base Case, using
typical values for
New York City subways... We
discovered in the Station-Stop
puzzle
that cruise speed vC does not
play a part in determining
minimum headway tH. The Trip
Time puzzle was a
different matter.
There we ascertained the time between stations tS,
noting
that if the distance between stations xS
is large, as with
long-haul railroad services,
tS will approach xS /
vC.
Passenger transit systems, especially in urban
environments, will typically
require xS to be less than a couple of
miles, which brings into consideration
parameters other than vC for calculating
Trip
Time. Here is a Base Case, using
typical values for
New York City subways...
-
Train Length: xL
= 510 ft (10-car consist
of R142 vehicles, each 51 ft long)
-
Cruise Velocity: vC = 50 mph
(73.3 fpsps)
-
Platform Velocity: vP =
30 mph (44.0 fps)
-
Normal Acceleration: aS
= 2.5 mphps (3.7 fpsps)
-
Service Braking Deceleration: dS
= 3.0 mphps
(4.4 fpsps)
-
Feathered Stop Decleration: dF
= 1.5 mphps
(2.2 fpsps)
-
Dwell Time: tD = 20
seconds
Using the values indicated above, puzzle
solvers calculated
that the time a train spends executing a station-stop tSS
= 96 seconds, over a distance of xSS =
2,639 feet.
The time required for an express train traveling at vC
= 50 mph
(73.3 fpsps) to cover that same distance without
stopping is tBYPASS
= 36 seconds. Thus, the difference in Trip
Time tDELTA enjoyed by an
express train in bypassing
a local station tDELTA = tSS - tBYPASS
= 1
minute.
 Our
Express
vs Local puzzle
posed the question,
"What are the real payoffs
attributable to express
service?" There can be no doubt that
for transit passengers,
especially commuters, any
payoff must take
the form of reduced
Trip Time. Getting
from Station A to Station B -- that's all that
matters. Quicker the better.
The solution might seem to be Trip
Time
savings for passengers on express trains, amounting
to about a minute
for every bypassed station. Oh, but there is
more to the subject. Our
Express
vs Local puzzle
posed the question,
"What are the real payoffs
attributable to express
service?" There can be no doubt that
for transit passengers,
especially commuters, any
payoff must take
the form of reduced
Trip Time. Getting
from Station A to Station B -- that's all that
matters. Quicker the better.
The solution might seem to be Trip
Time
savings for passengers on express trains, amounting
to about a minute
for every bypassed station. Oh, but there is
more to the subject.
The graph below is called a "string
chart." This
one shows four theoretical subway stations with local
and express trains that
have been modeled
using the
Base Case parameters developed above.
Various times
and distances are indicated on the graph.
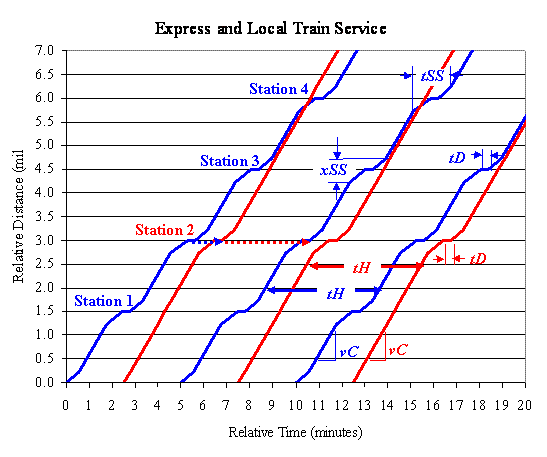 Here are some observations...
Here are some observations...
-
Three stations (1, 3,
4)
have local train service only.
-
One station (2)
has both
local and express service.
-
By assumption, the distance between
stations xS
= 1.5 miles.
-
Both train services are assumed to be
running on five-minute
headways,
tH = 5 min.
-
Average wait for a local train at any
station ("boarding
delay")
tBD = tH / 2.
-
Average wait for an express train at
an express station ("boarding
delay") tBD = tH / 2.
-
Arrival times at station 2
are staggered, with the local
train arriving
a minute ahead of the express
train.
-
Passengers changing trains from local
to express will have
to wait about a minute.
-
Passengers changing trains from express
to local will have to
wait about four minutes.
-
Average wait ("cross-platform delay")
tXP = (1
+ 4) / 2 = 2.5 min (tH / 2).
-
Trip Time
between local stations
tS
= tSS + (xS - xSS) / vC
= 168
sec (2.8 min).
-
Express trains bypass local stations,
saving one minute of
Trip
Time per station.
-
Trip Time
between express stations
bypassing n local stations tS
= tSS +
(n
xS - xSS) / vC
No more than one train can be operating in
the trackage between
local stations. On a fixed-guideway transit system with
express and local
train service, the quickest Trip
Time means
more than merely getting on-board at A and getting
off-board at B.
Commuters must make choices. Let's see how well
the following five
categories work in analyzing those choices:
Passenger
Category
|
Departure
Station
|
Enroute Narrative
|
Destination
Station
|
|
1
|
Express
|
Ride express train. Bypass all
local stations. |
Express
|
|
2
|
Local
|
No more than one express station
between depature and
destination. Ride local train, which stops
at all stations. |
Local
|
|
3
|
Local
to
Express
|
Ride local train.. Change
trains at express station.
Stop only at express station(s), bypassing local
stations. |
Express
|
|
4
|
Express
|
Stop only at express station(s),
bypassing local stations.
Change to local train, which stops at local
station(s). |
Express
to
Local
|
|
5
|
Local
to
Express
|
Stop at all station(s).
Change to express train.
Stop only at express station(s), bypassing local
stations. Change
to local train, which stops at local station(s) |
Express
to
Local
|
-
Category 1 Passengers, with
routes between two express
stations will surely choose to ride express trains
and enjoy a reduction
in overall Trip Time
by about one minute per
bypassed station.
-
Category 2 Passengers,
traveling between local stations,
will not be able to make use of express train
service unless two or more
of the enroute stations having express service,
which would then put those
passengers in Category 5.
-
Category 3 Passengers must
board a local train and,
for destinations at express stations, with routes
that include two or more
express stations, can choose to change trains
enroute to bypass local stations.
-
Category 4 Passengers,
departing at an express station,
with routes that include two or more express
stations, can choose to board
an express train and bypass local stations, but must
then change trains
to reach destinations at local station.
-
Category 5 Passengers must
board a local train and,
with routes that include two or more express
stations, can choose to change
trains and bypass local stations, but then must
change trains again to
reach destinations at local stations.
A passenger in any of the five categories
will suffer an
average boarding delay tBD = tH
/ 2.
Or maybe longer...
Consider a Category 1 or 4
Passenger arriving
at the departure platform just as the express train
pulls out of the station.
Suppose also that a local train is just pulling
in. The choices would
be to leave right away on the local train or to wait
for as long as tBD
= tH to board an express train
Whenever there is a choice that
requires changing train
enroute, cross-platform delays impact Trip Time and
reduce the benefits of express service.
Category 3 and 4 Passengers
will suffer tBD = tH /
2 plus a cross-platform
delay tXP =
tH / 2.
Category 5 Passengers will suffer two
cross-platform
delays for a total of tH.
Thus, for example,
with a headway
tH = 5 min, Category 5 Passengers will
wind
up riding an express train that must bypasses seven
local stations
just to break even.
 Discerning
the real payoffs attributable to
express service
calls for 'reverse engineering' an extant subway
system. Ascertaining
the benefits for passengers will necessitate
answering statistical
questions about the travel patterns of commuters in each
category.
And something else... Discerning
the real payoffs attributable to
express service
calls for 'reverse engineering' an extant subway
system. Ascertaining
the benefits for passengers will necessitate
answering statistical
questions about the travel patterns of commuters in each
category.
And something else...
The savings in Trip Time
attributable to express train service will depend on
the number n
of local stations bypassed between successive
express stations.
Exclamation Point Alert: The New
York subway map
shows
n varying from seven (1 case) all
the way down
to
zero (7 cases)! Indeed, for all
five lines, there
are a total of 27 pairs of express stations between
which there are a total
of 46 local stations, for an average number of
'bypassable' local stations
n
= 1.7.
To justify the investment, there must
be some other real
payoffs attributable to express service beyond
those for
passengers. How about another kind of speed: flow-rate?
Not
miles-per-hour as experienced by passengers
but speed measured as
passengers-per-hour achieved by
stations. A transportation
system is not just about getting people from A to B
quickly but getting
the most people loaded at A and ultimately
unloaded at B -- and
C and D -- whatever the Trip
Time over
each individual route.
 Two
clues for this speculation: [1] that, as described
above, there are so
few local stations situated between express stations
ready to be bypassed
by express train service (n = 1.7) and
[2] that express stations
often serve sites that produce and absorb high volumes
of patrons (Grand
Central Terminal, Pennsylvania Station, Rockefeller
Center, Times Square).
Having both express and local service, an express
station will handle twice
the
volume of passengers. Never mind that
some express train
passengers cannot access local stations for their
destinations. Two
clues for this speculation: [1] that, as described
above, there are so
few local stations situated between express stations
ready to be bypassed
by express train service (n = 1.7) and
[2] that express stations
often serve sites that produce and absorb high volumes
of patrons (Grand
Central Terminal, Pennsylvania Station, Rockefeller
Center, Times Square).
Having both express and local service, an express
station will handle twice
the
volume of passengers. Never mind that
some express train
passengers cannot access local stations for their
destinations.
Exclamation Point Alert: Today
there is an alternative
for handling twice the volume! Modern transit
systems do not need
to budget for all those construction expenditures to
double each rail line
to provide express trackway, including all those
requisite tunnels and
all those extra platforms at each express station,
along with extra street-level
entrances, extra stairways and escalators for
circulation between concourses
and platforms.
A comparable benefit in system
flow-rate would
accrue to all stations by running more
trains with closer
headways. Oh right, the New York Subway
system applies 'legacy
technologies' dating back a century or more.
Closer headways require
modern systems, specifically automatic train control.
Even so, solvers of this puzzle will also
notice that wherever
tS
< tH a simplified train control
algorithm can be applied:
Each train would be held at a given station until the
station ahead is
clear. Moreover, with a guarantee that the next
station is unoccupied,
certain buffer distances can be reduced to zero.
That will
allow an improvement in Trip Time
by as much as 8.5 seconds in the Base Case
model while reducing
the benefits of express train service by more
than four seconds
per bypassed station.
Accordingly, let us take as our
solution for the Express
vs Local puzzle...
Real
payoffs attributable to express
service are...
-
reduction
of one minute of Trip Time
for each bypassed station and
-
doubling
of flow-rate at express stations
for a given headway.
|
|
 We
discovered in the Station-Stop
puzzle
that cruise speed vC does not
play a part in determining
minimum headway tH. The Trip
Time puzzle was a
different matter.
There we ascertained the time between stations tS,
noting
that if the distance between stations xS
is large, as with
long-haul railroad services,
tS will approach xS /
vC.
Passenger transit systems, especially in urban
environments, will typically
require xS to be less than a couple of
miles, which brings into consideration
parameters other than vC for calculating
Trip
Time. Here is a Base Case, using
typical values for
New York City subways...
We
discovered in the Station-Stop
puzzle
that cruise speed vC does not
play a part in determining
minimum headway tH. The Trip
Time puzzle was a
different matter.
There we ascertained the time between stations tS,
noting
that if the distance between stations xS
is large, as with
long-haul railroad services,
tS will approach xS /
vC.
Passenger transit systems, especially in urban
environments, will typically
require xS to be less than a couple of
miles, which brings into consideration
parameters other than vC for calculating
Trip
Time. Here is a Base Case, using
typical values for
New York City subways...

 Discerning
the real payoffs attributable to
express service
calls for 'reverse engineering' an extant subway
system. Ascertaining
the benefits for passengers will necessitate
answering statistical
questions about the travel patterns of commuters in each
category.
And something else...
Discerning
the real payoffs attributable to
express service
calls for 'reverse engineering' an extant subway
system. Ascertaining
the benefits for passengers will necessitate
answering statistical
questions about the travel patterns of commuters in each
category.
And something else...