Air-Race -- Puzzle

Air-Race

+++

Chapters in the sky features a certain Cardinal 177 RG, shown in this snapshot taken near
Cabo San Lucas at the tip of Baja California during the Total Solar Eclipse July 11, 1991.

Cardinal 177 RG Performance – Gear and Flaps Retracted
Maximum Cruise Speed	*vMX*	165 KIAS	KIAS = knots indicated airspeed; KTAS = knots true airspeed *KTAS = KIAS + k h* *0.0013 < k < 0.0023 kt/ft*
Minimum Drag Speed	*vMD*	90 KIAS
Never Exceed Speed	*vNE*	200 KIAS
Stall Speed	*vSS*	60 KIAS
Service Ceiling	*hSC*	15,500 ft MSL	*for h = hSC and v = vSS,* *rC = 0*
Seal Level Rate of Climb	*rC0*	700 ft/min	*for h = hSC and v = vSS,* *rC = 0*

Question: For winning an Air-Race, what is the best cruise altitude?

The question seems simple enough. Each segment of a race course is defined by fixes on the ground. The shortest distance between them, of course, is a straight line. The table above shows what every pilot knows -- that true airspeed increases with altitude. Now, in the absence of wind, ground speed equals true airspeed. So, the answer to the question is higher the better.

Not so fast. Higher the cruise altitude the longer it takes to climb up there.

Let us suppose that a hypothetical Air-Race is to be conducted. There is only one 'segment', between fix f1 and fix f2, which is 290 nautical miles toward the east. After take-off each plane flies over f1 at pattern altitude hPA = 1,000 ft MSL, where the time-of-day is logged by officials on the ground. At the end of the segment, each plane flies over f2 at hPA = 1,000 ft, where the time-of-day is logged. The elapsed times between fixes determines the winner of the Air Race.

Two identical Cardinals show up for the Air-Race. Both pilots have nicknames, which correspond to the livery of their respective planes, Red and Blue.

At the pre-race weather briefing, the pilots are informed that winds are calm over the entire segment and that sky conditions are CAVU. The navigation charts indicate that foothills along the route have elevations up to 4,500 ft MSL. By the way, under VFR, the 'hemispheric rule' applies, which, for easterly headings, flights must use cruise altitudes of 'odd-numbers of thousands plus five-hundred feet'. During the meeting, the two Cardinal pilots comment that this occasion offers an ideal opportunity to address the question in the Air-Race puzzle above.

Red elects to cruise at 5,500 feet to clear the hills, and Blue agrees to fly 6,000 feet higher, cruising at 11,500 feet. After shaking hands, they proceed to the flight line.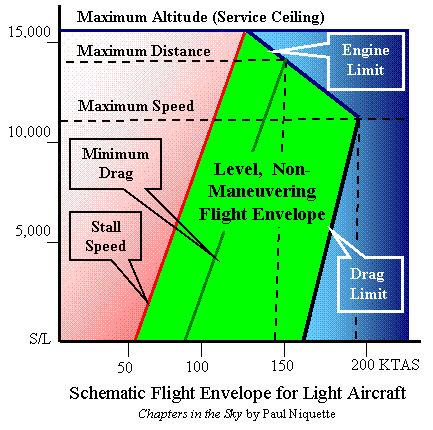

Solvers of the Air-Race puzzle are invited to review typical aircraft performance limits as depicted in the schematic on the right and explained in an entry entitled Flight Envelope.

Within the envelope, an aircraft's performance figures ('V-speeds') are what the pilot finds indicated by panel instruments -- regardless of atmospheric realities like temperature and altitude. Thus, for example, to derive any true airspeed reading...

KTAS = KIAS + 0.0023 h

...is a simple expression based on Standard Atmosphere for use here.

Nota bene, in the absence of wind, ground speed = KTAS.

Along the 'drag limit' line, the maximum cruise speed vMX in level flight is adversely affected by 'volumetric efficiency' of the engine with increasing altitude, such that the more appropriate expression is...

KTAS = KIAS + 0.013 h

Finally, one might observe that 'service ceiling' is the altitude MSL at which the 'rate of climb' rC is reduced to zero even with the plane slowed almost to stall speed vSS.

Solvers of Green Flight will recall that 'minimum drag speed' vMD is typically about 30% faster than vSS, and vMD is also the speed for 'best rate-of-climb' at all altitudes.

GO TO SOLUTION PAGE