 Copyright ©2017 by Paul Niquette. All rights reserved. |
|||||
 The
sketch below depicts planet p2 as
if it were in orbital isolation, being acted upon
only by the sun's gravitational force f2(r)
and by centrifugal
force f2(ω,r). That condition prevails for nearly all of
its orbit, but when it comes alongside p1
or p3 in their adjacent orbits, p2
will necessarily change its orbit in response to
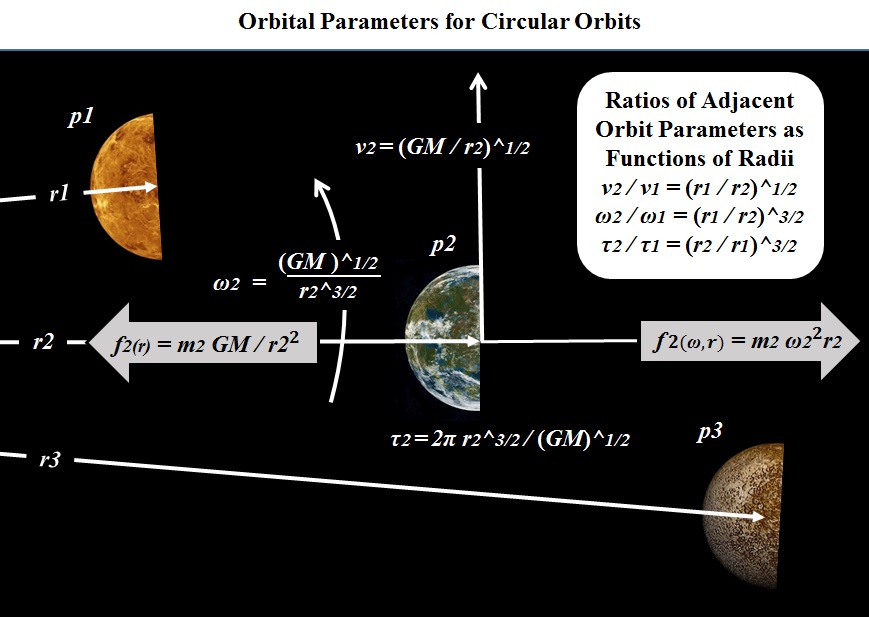their gravitational forces.  The puzzle challenges solvers to start with three exoplanets in circular Trappist Orbits and to show how each will remain stable for some indefinitely long period of time. We have seen in the sketch reprised below how those gravitational forces f12 and f23 can be decomposed into their respective Tangential and Radial components... 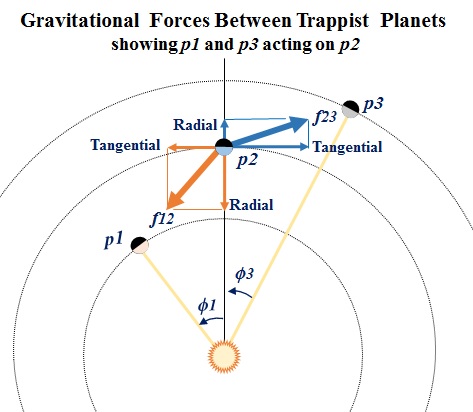 Tangential and Radial components for gravitational force f12 are shown below as functions of Time. 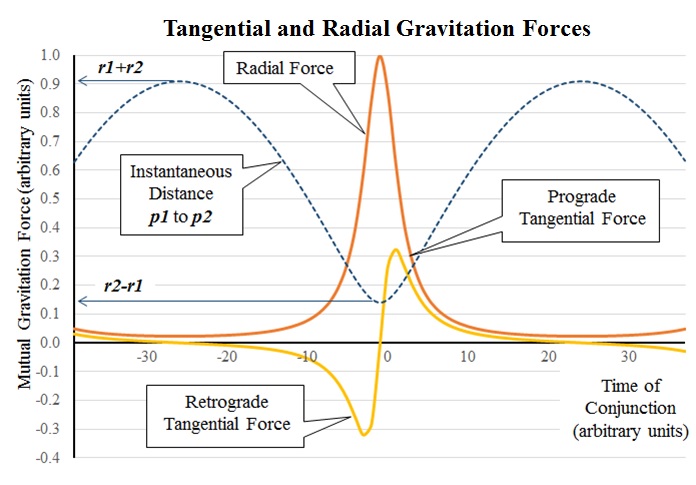 The Tangential component of f12 prior to each least separation acts on p2 as a Retrograde force, which after the least separation changes to an equal and opposite Prograde force. The net effect is that p2 neither accelerates nor decelerates at each passing of p1. Same for each passing of p3. The Radial component of f12 is another matter indeed. It reaches its peak at the least separation where r21 = r2 - r1. r21 = r2-r1 Integrated over the 'duration of proximity' (-20 < t < +20), its effect would seem to be the application of an impulse vector (j12 = ∫ f12 dt) pulling p2 toward the sun distorting p2's orbit, as if -- intuitively speaking -- the sun's gravity gets momentarily increased by p1's gravity added to it. But no... Intuition be damned.As suggested in the Trappist Orbits puzzle each point of least separation with an adjacent planet (p1 or p3) can be regarded as a maneuver node, and in place of thrust vectors, think components of the gravitational force between planets. The 'radial-in' component of p1's gravity force will rotate p2's orbit in its plane through some angle in the direction of planet motion. The effect may be described as and increment of orbital 'precession' in prograde. Same for the 'radial-out' component of p3's gravity force, except that p2's orbit will be rotated through some angle opposite to p2's motion. Hey, the postulated orbits are circular. Rotating a circle around its center either way will not change its shape. Duh. All three orbits will be stable for billions of years! Does that mean we have solved the Trappist Orbits puzzle? No. The
present Trappist Orbits are
not perfectly circular. For the first three
planets, we observe eccentricities range between 0.003
and 0.019. One might suppose that at some distant
past, they may have been less circular -- that over time
gravitational forces have acted to reshape their
orbits. Let us test that supposition by letting e1
= e2 = e3 = 0.065. 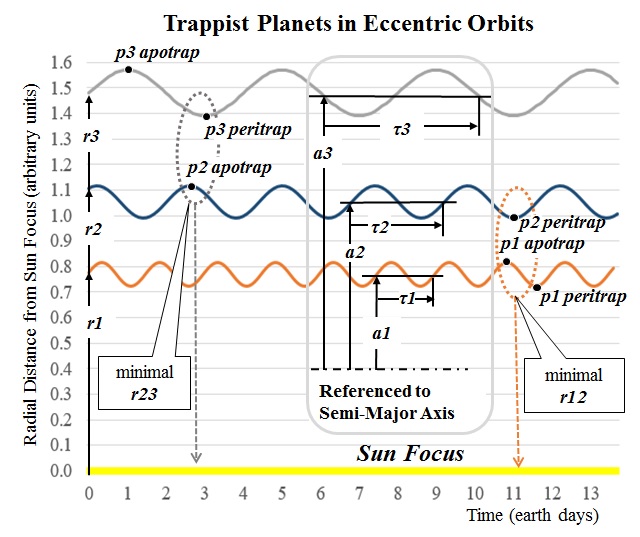 At t ≈ 2.8, if planet p2 happens to be passing through p2 apotrap at that time and p3 happens to be passing through p3 peritrap at the same time, the distance between p2 and p3 will be near minimum and the gravitation attraction between p2 and p3 will be near the absolute maximum.The latter case resembles the sketch below reprised from the Trappist Orbits puzzle (t = 0). The radial-in force on p2 rotates its orbit counterclockwise while the radial-out force on p1 rotates its orbit clockwise. We observe that p2 peritrap rotated ccw and p1 apotrap rotated cw are no longer aligned with each other, so the conditions described above for t ≈ 11.1 cannot be duplicated -- until the orbits get rotated in opposite directions all the way around to meet again. 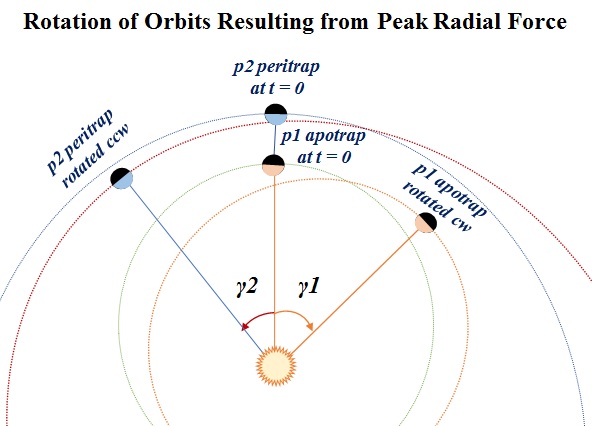 In
between orbital re-alignments, the planets keep up
their respective orbital motions, passing each other
at various distances and exerting commensurate
gravitational forces upon each other. The
sketch below derives the total mutual gravitational
force on planet p2 as the sum of f12
and f23. The two cases of maximal radial forces described above ( t ≈ 2.8 and t ≈ 11.1) can be seen highlighted. 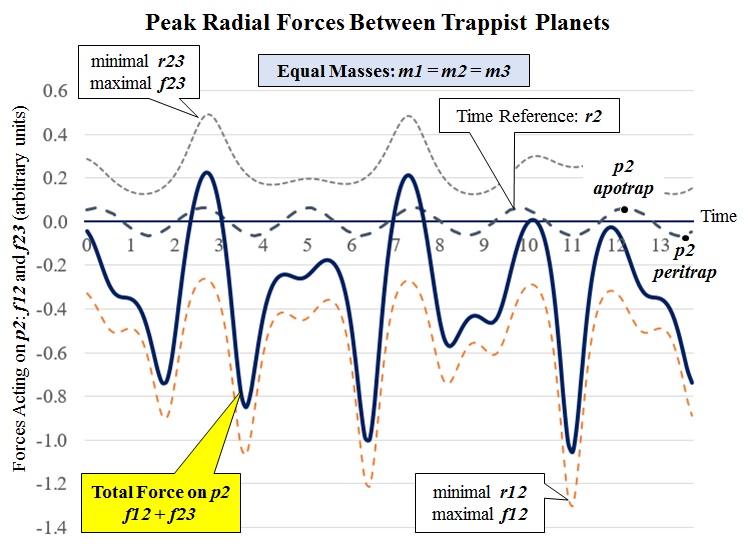 Conclusion: The planet p2 is acted upon by an irregular -- some might say 'chaotic' -- sequence of gravitational forces by planets p1 and p3, favoring radial-in more than radial-out. But so what? Stand by for exclamatory sentences.With or without what is called orbital resonance, radial forces... ...imposed on a planet by a planet in an adjacent orbit can only rotate the orbit in its own plane!Therefore...
Challenging
the existence of orbital resonance
The mutual gravitational attraction between two planets passing each other in adjacent orbits can be decomposed into three vectors in space. They are analogous to the orthogonal forces produced by spacecraft thrusters at a ‘maneuvering node’ (http://wiki.kerbalspaceprogram.com/wiki/Maneuver_node): [1] ‘prograde/retrograde’ appear in succession in opposite directions during the passing and thus cancel each other out; [2] ‘normal/anti-normal’ can change the orbital inclination but would have negligible effect for coplanar orbits; and [3] 'radial-in/radial-out' reaches a maximum at conjunction of the planets and will have no effect on the shape of each orbit but will rotate both orbits in their own planes, moving the apoapses and periapses in opposite directions around their respective ellipses. The ratio of orbital periods has nothing to do with those three effects, which puts the whole subject of ‘orbital resonance’ in doubt. Surely there must be plenty of authoritative references that establish this reality.
|
