Trappist Orbits

Copyright ©2017 by Paul Niquette. All rights reserved.

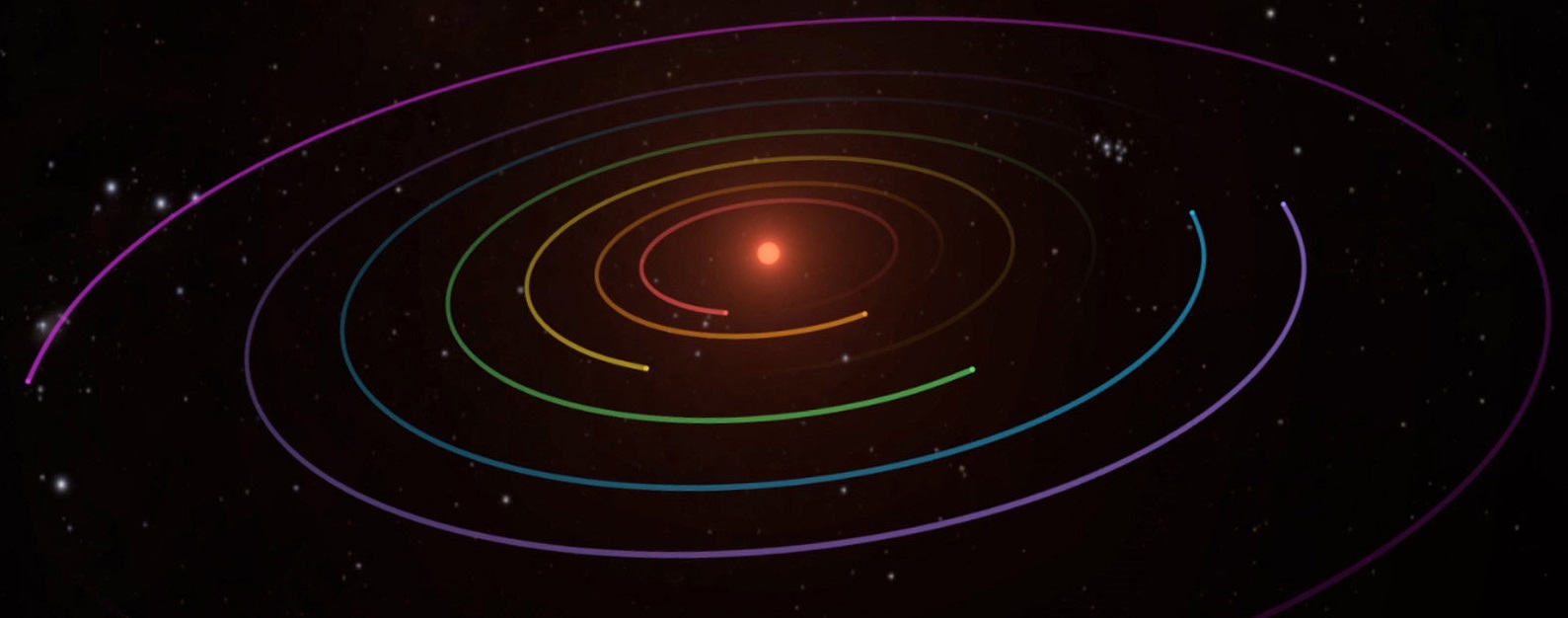
A visualization of the seven planets orbiting the star TRAPPIST-1.
NASA/JPL/Caltech

Twenty-five years ago, all the known planets were in our own Solar System.  Until 1992, exoplanets were the stuff of speculation.  Thanks to advances in detection methods, as of this writing (May 2017), more than 3,600 exoplanets have been confirmed in more than 2,700 planetary systems, and there are billions more to be found in just the Milky Way Galaxy.

TRAPPIST (Transit Planets and Planetesimals Small Telescope) is the name for a pair of robotic telescopes that made the initial discovery in 2015 of...

TRAPPIST-1 is an exceptional planetary system surrounding an ultra-cool dwarf star, which is about the size of our own planet Jupiter but situated 40 light-years away in the constellation of Aquarius .

Exceptional indeed, inasmuch as TRAPPIST-1 comprises a total of seven temperate terrestrial exoplanets -- the most found in any exoplanet system discovered so far.  They are tightly packed, with all seven planets whirling through space well within the orbital dimensions of our planet Mercury.

For the Trappist Orbits puzzle, let us name the planets p1, p2, p3, ... p7, and observe...

• Orbital periods ('years') τ1, τ2, τ3, ... τ7 range from 1.5 to 18.8 earth days.   
• Orbital radii r1, r2, r3, ... r7 range from 1.66 to 8.92 Mkm (1.0 to 5.6 Mmi).
• Orbital proximities range from r2-r1 = 0.62 to r7-r6 = 2.07 Mkm (0.4 to 1.3 Mmi).
• Orbital eccentricities e1, e2, e3, ... e7 are all less than 0.09 -- essentially circular.

Orbital Resonance

Close as they are to each other, the TRAPPIST-1 planets have not collided for the last few million years.  The seven orbits appear to be 'stable' -- even harmonious...

The Harmony That Keeps Seven Earth-size Worlds From Colliding

The linked reference postulates that orbital resonance plays a key rôle in assuring 'harmony' among the seven planets in the Trappist Orbits.

It is easy to show that adjacent Trappist Orbits have periods that are ratios of small whole numbers and thus meet the criterion for orbital resonance...

Consider the first three Trappist Orbits: τ1 = 1.511, τ2 = 2.422, τ3 = 4.050 earth days...

          τ2 / τ1 = 1.603 versus 8/5 = 1.600 -- 99.8% agreement
          τ3 / τ2 = 1.672 versus 5/3 = 1.667 -- 99.7% agreement

...therefore, while p2 completes 5 orbits, p1 completes 8 orbits and p3 completes 3 orbits.

Sure enough, using gazillions of simulations on a supercomputer, astrophysicists have tested the 'harmony' concept and confirmed that the present configuration of Trappist Orbits will be sustainable for billions of years.  This puzzle will use a simple spreadsheet to do the same...

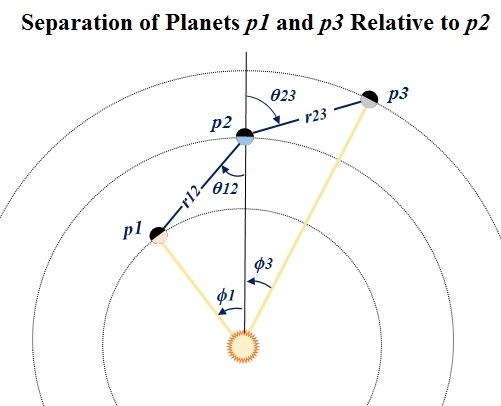
Here is a snapshot of the first three planets in circular counterclockwise orbits around TRAPPIST-1.   We observe that p1 has recently passed p2 where r12 = r2 - r1, and p2 has recently passed p3, where r23 = r3 - r2.  Solvers can use this sketch to derive the distances r12 and r23, which by Newton's Law determine the instantaneous gravitational forces acting between the planets...



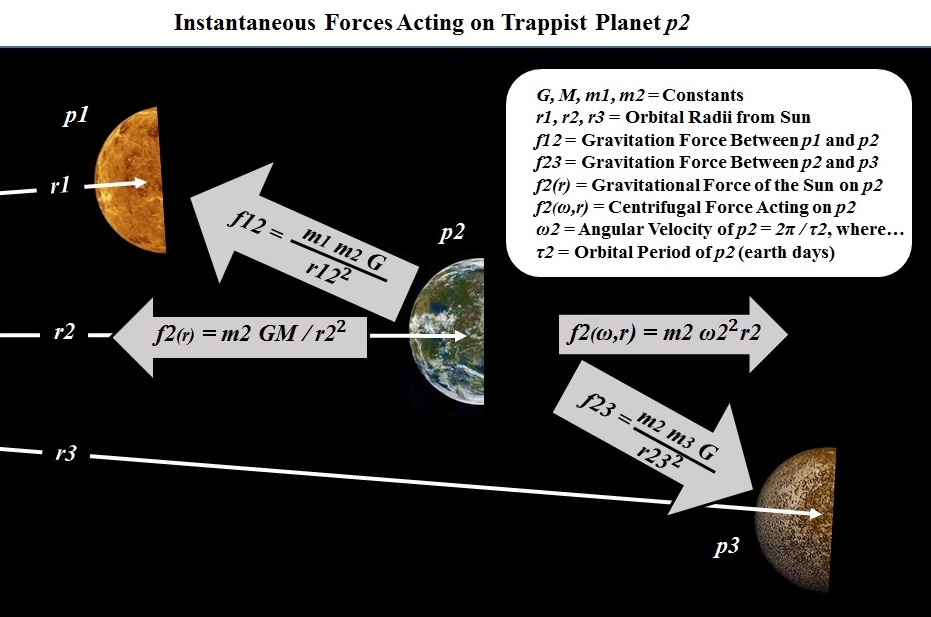
Four forces are shown acting on p2:  Gravitational force f2(r) imposed on p2 by the sun and  varies inversely with the square of the orbital radius r2².  Centrifugal force f2(ω,r) r2 and with the square of the angular velocity ω2². For a circular orbit f2(r2) = f2(ω2,r2), thus ω2 = (GM)^1/2 r2 ^-3/2.

Planets p1 and p3 in adjacent orbits impose gravitational forces f12 and f23 on p2, which vary inversely with r12² and r23².  As planet p1 passes below p2, ϕ1 = 0, r12 decreases to its minimum, r12 = r2 - r1, and f12 reaches its maximum, f12 = m1 m2 G / (r2 - r1)².  Likewise, as planet p2 passes below p3, ϕ3 = 0,  r23 decreases to its minimum, r23 = r3 - r2, and f23 reaches its maximum, f23 = m2 m3 G / (r3 - r2)².

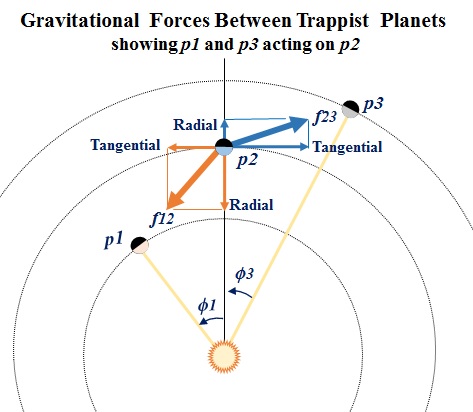
This sketch shows f12 and f23 each decomposed into their respective Tangential and Radial components.  We observe that...

Planet p1 has recently passed below p2, and its gravitational force f12 is now acting to accelerate p2 tangentially along its orbital path while simultaneously pulling p2 radially toward the sun.

Planet p2 has recently passed below p3, and its gravitational force f23 is now acting to decelerate p2 tangentially along its orbital path while simultaneously pulling p2 radially away from the sun.

Newton's Third Law of Motion, of course, assures that f12 and f23 apply to p1 and p3, respectively, in equal magnitudes and opposite directions.

Before taking on the challenge in the Trappist Orbits puzzle, some solvers may need to be advised that in orbital mechanics, the motions of celestial bodies resulting from applied forces are counter-intuitive.  Accordingly, we need to indulge in some orbital mechanics here...

We might acquire an understanding of the subject at Kerbal Space Program, which provides a practical treatment of maneuver nodes in rocketry.  Maneuver nodes are defined as planned orbital locations where thrust vectors are prescribed to accomplish various objectives: transfer orbit, circularization, rendezvous, station-keeping.  Solvers may regard the 'points of least separation' between adjacent planets as 'spontaneous maneuver nodes' and treat the components of gravitational attraction between planets as if they were orthogonal thrust vectors as produced in command modules and artificial satellites...

From a circular orbit, a brief Tangential force applied in the same direction as a satellite's motion ('prograde') changes the orbit to elliptical; the satellite will ascend and reach the highest orbital point (the apoapse) at 180 degrees away from the point of application ('firing point' in rocketry); then it will descend back, returning to the firing point.  So too, thrust applied in the opposite direction of the satellite's motion ('retrograde') changes the orbit to elliptical with the lowest orbital point (the periapse) at 180 degrees away from the point of application; then it will ascend back, returning to the firing point.

From any location in an elliptical orbit, a brief Radial force applied toward the focus of the orbit -- the sun -- rotates the whole orbit in its plane through an angle in the direction of the satellite's motion, thereby moving both the apoapse and the periapse to new locations still opposite to each other.  The effect is generally described as orbital 'precession'.  A brief force applied away from the focus of the orbit ('radial-out') rotates the orbit in its plane through an angle in the opposite direction from the satellite's motion, as illustrated in the sketch below...

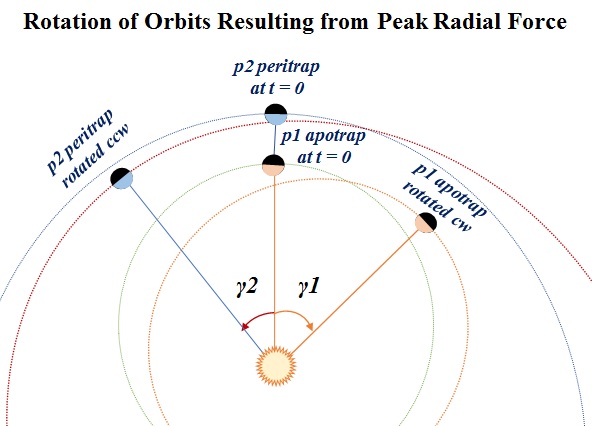
In the sketch above, we have coined the terms 'apotrap' and 'peritrap' for the Trappist Orbits puzzle.  Whenever the elliptical orbits of p1 and p2 happen to become aligned, such that p1 passes its p1 apotrap just as p2 simultaneously passes its p2 peritrap directly above, then r12 reaches its absolute minimum, which results in radial force f12 reaching its absolute maximum.  The p2 orbit rotates in its plane through some angle γ2 in the direction of the planet motion, as indicated by p2 peritrap rotated ccw.  Meanwhile, being acted on equally in the opposite direction, the p1 orbit rotates in its plane through some angle γ2 in angle γ1 in the direction opposite to the planet motion, as indicated by p1 peritrap rotated cw.

---

Solvers are invited to make the following simplifying assumptions: Three exoplanets p1, p2, p3 are in circular, coplanar orbits at radii r1, r2, r3 , such that in the time p2 takes to complete 5 orbits, p1 completes 8 orbits and p3 completes 3 orbits.

Show that each orbit will remain stable for some indefinitely long period of time.

GO TO SOLUTION PAGE