Strange Series Solution

Strange Series

s observed in the puzzle set-up, the generating formula for this Strange Series is extremely simple (n / 2 | 3n + 1) and seems to imply unbounded growth. However, a maximum value is always reached -- a numerical mountaintop, so to speak, after which the algorithmic terrain resembles a jagged cliff, plummeting toward the integer 1, there to bump along endlessly 1, 4, 2, 1...

The summit reached by the Strange Series depends on the initial integer or 'seed' (to mix metaphors). Here is the plot of a numerical sequence that reaches a maximum of 9,232, starting with a seed of 27. Let's call it the 27|/\|9,232 series...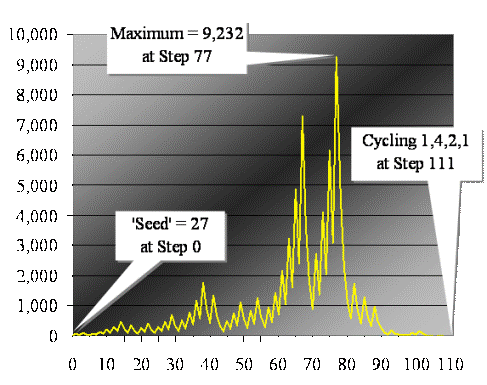

Of course, if any of the 76 integers in the 27|/\|9,232 series were to be used as a 'seed', the same peak would be reached. The integer 27 happens to be the first entry on the puzzle-list. That may also be your first clue for the solution.

Since 27 is odd, we apply 3n +1 and getting 82 for the second in the 27|/\|9,232 series. Lo and behold, 82 is on the puzzle-list. Since 82 is even, we apply n / 2 to get 41, the third integer in the 27|/\|9,232 series, and we find that 41 is also on the puzzle-list. Seems like we are on to something here.

A quick count turns up 157 entries in the puzzle-list. If they are all supposed to be generated by the Strange Series in the 27|/\|9,232 series, where do those extra 81 entries come from?

Sophisticated solvers will notice that for any integer value of n, the expression 3n + 1 will always produce an even number. The next entry in the sequence will always apply the expression n / 2, which can produce either an even or an odd integer.
Accordingly, there is only one way that the Strange Series can generate an odd integer, always by virtue of n / 2, but an even integer may be reached two ways: from below by 3n + 1 for any value of n or from above by n / 2 whenever n is divisible by 4, 8, 16, 32,...

The next integer in the 27|/\|9,232 series after 41 is 124, which is produced by 3n + 1, also appears on the puzzle-list. But 124 might also be produced by n / 2 from 248, which is also on the puzzle-list. Thus as a 'seed', 248 will lead to that peak of 9,232; however, 248 cannot itself be generated by the Strange Series from any of the 76 integers in the 27|/\|9,232 series. Maybe 248 does not belong on the puzzle-list and neither do the rest of those 81 extra entries, under the supposition that they, too, cannot be generated by the Strange Series from any of the 76 integers in the 27|/\|9,232 series.

ot a bad supposition, comma, but...

The question in the puzzle reads, "Which 'seed' [singular] does not belong on this list?" Accordingly, maybe we should try to find one entry on the puzzle-list that does not lead to that peak of 9,232. Testing each entry is laborious, even using a spreadsheet. Nevertheless, along the way, the patient solver will discover another property in the Strange Series -- a strong resistance to producing a numerical mountain higher than 9,232. Other peaks (808, 2,536, 4,372) are like foothills, until...until ...

The smallest 'seed' that can break through that 9,232 barrier is 793, and it generates an integer sequence that soars all the way up to 39,364, as plotted below...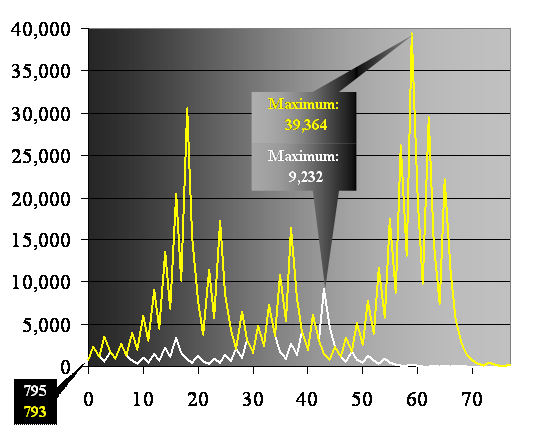

Ironically, 795, which is slightly larger than 793, will generate a sequence that leads to that old 9,232 peak, along with all the other entries on the puzzle-list. Accordingly, the solution to the Strange Series puzzle is...

793

Epilog: Some fourteen years after the publication of Strange Series, a well-produced video...

The Simplest Math Problem No One Can Solve

...came along. It explores many properties of (n / 2 | 3n + 1) beyond the few that were independently discovered above by your puzzle-master. Seems that just about every mathematician in history has tried in vain to prove what has become known as the Collatz Conjecture.

Home Page

Puzzle Page

Math and Models

The Puzzle as a Literary Genre