certain puzzler came across a file in his "Idea" folder
that reads, "Start with any integer, n.
If n is even, divide it by two; if n
is odd, multiply it by three and add
one. Repeat the process to generate a Strange Series of
integers."
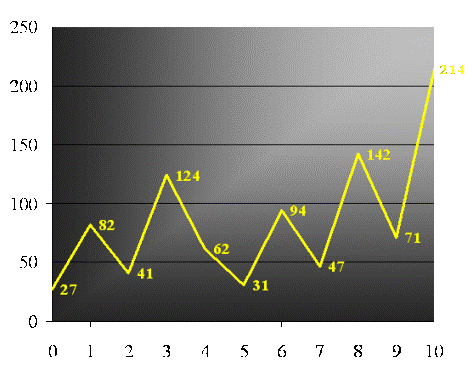
An example in the file started with a 'seed' number n = 27 to produce a sequence of integers as follows: 82, 41, 124, 62, 31, 94, 47, 142, 71, 214... They are shown graphically below. 
Starting with n = 35 or n = 53, the limit is the same, 160. Now, increase the 'seed' from n = 53 to n = 54 and you produce a series that ascends all the way up to a peak of 9,232 before descending back down to the 1, 4, 2 oscillation. Taken together,
those facts and features may be enough to warrant the
cryptic title found in that long forgotten file: "Strange Series." An
exclamation point may also be warranted, but you are
advised to postpone that until after solving the
puzzle...
|
ontinuing the
series for another 67 steps, the formula finds that
the numbers reach a maximum of 9,232, then decreasing
in an irregular way, winding up -- 'down', actually --
in the 111th step at
the integer 1, then cycling repeatedly through three
values 4, 2, 1, 4, 2, 1,... By experimenting
using a spreadsheet, you will find that every 'seed'
produces a sequence with an upper limit. For
example, n = 79 reaches a maximum of
808. 