 Trains,
planes, and automobiles – they all carry passengers, which necessitates
stopping from time to time. In railroading, headway is determined
by station stops.
Some people may be astonished to learn that headway has nothing to do with
"safe following distance" at crusing speed along trackways and tunnels.
The previous sentence deserves exclamatory punctuation, as we shall see. Trains,
planes, and automobiles – they all carry passengers, which necessitates
stopping from time to time. In railroading, headway is determined
by station stops.
Some people may be astonished to learn that headway has nothing to do with
"safe following distance" at crusing speed along trackways and tunnels.
The previous sentence deserves exclamatory punctuation, as we shall see.
The sketch below is a 'phase-plane' plot, same
as used in the solution to the Trail Braking
puzzle. We observe a train-in-trail approaching a station at cruise
speed
vC. As a practical matter, trains cannot be operated
in stations at full cruise speed vC. Imagine the danger
to passengers waiting on the platform when a train comes barreling into
the station at, say, 80 miles per hour.
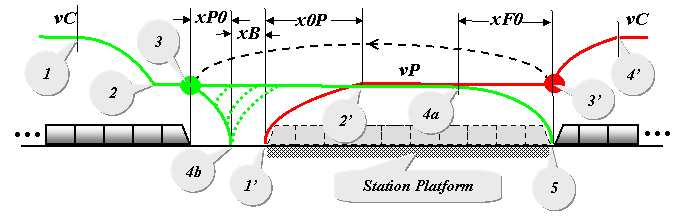
Accordingly, wayside signage or the train control
system at Point 1 will command the train to slow down. At Point 2, the
train has slowed to vP , "platform operating speed," let's
call it. Upon reaching Point 3 the train will be stabilized at vP,
ready to enter the station platform.
Prior to the arrival of the train-in-trail at Point 3,
the train control system will have routinely determined whether the station
platform is occupied by the previous train. The time-table, naturally,
will be designed to assure that the platform will
not be occupied
by the train ahead, so the train-in-trail will generally be allowed to
continue to into the platform at vP all the way to Point
4a.
Positioning a train with precision in a station platform
is more technically demanding than full service braking between stations.
For one thing, passengers standing in the aisles preparing to disembark
are susceptible to sudden changes in brake-rate ("jerk" is the technical
name for it) at the instant a train comes to rest. Limiting jerk
calls for what is called "the feathered stop." Beginning at Point
4a, deceleration must gradually be reduced as the train pulls into the
platform. The feathered stopping distance xF0
brings
the train to a halt with its lead car at Point 5.
Stopped in the station platform, a train waits out its "dwell
time" tD, during which doors are opened for unloading and
loading of passengers. Typically 20 seconds in duration, tD
must be added directly to headway.
In the sketch above, we now shift our attention
to Point 1', location of the rear-most extreme of a train as it is berthed
in the platform. When tD has elapsed, the doors are
closed and the train is dispatched to the next station. The train
accelerates at a constant rate aP to vP, the
platform operating speed, at Point 2'. As the tail car of the train
reaches the far end of the platform at Point 3', the train is released
to continue accelerating from vP to cruise speed vC,
which occurs well clear of the platform at Point 4'.
In a phase-plane plot, spatial positions are readily
discernible. Not so, instants in time. For example,
when the lead car of the train-in-trail is at Point
1, the tail car of the train ahead may be anywhere between Point
1' and Point 4' -- or beyond.
Prior to the arrival of the train-in-trail at
Point 3, the train control system has made a decision: If the station platform
is occupied by any part of the train ahead, full service braking will be
commanded at Point 3. The train-in-trail will begin decelerating
-- not from vC but from vP. That can
be accomplished at Point 4b, which allows for a buffer distance xB.
Here we note that xB defines an allowance for variations
in brake-rate. After stopping, the train-in trail must wait with
its lead car at Point 4b until the tail car of the train ahead reaches
Point 3', after which the train-in-trail will be released to accelerate
back up to vP for entry into the station platform.
Thus, it is fair to say that fixed-block realities encountered
in the solution to the Trail Braking puzzle
always apply at a Station Stop -- including
the "brick wall assumption." That will
be true even for so-called "moving-block" train control technologies.
Each of the distances shown in the sketch and
their respective time intervals may be derived as follows:
xB = 1,000 ft (assumed)
xP0 = vP2 / 2 dS
x0P = vP2 / 2 aS
xF0 = vP2 / 2 dF |
tB = xB / vP
tP0 = vP / dS
t0P = vP / aS
tF0 = vP / dF |
For estimating minimum headway, then, we focus
our analysis on Point 3 and Point
3', postulating their occurences at the same time -- at the same
time,
but for different trains. Suppose that when the lead car of
the train-in-trail reaches Point 3, the tail
car of the train ahead is just reaching Point 3'.
The question then becomes, how much time after that does it take
for...
[a] the lead car on the train-in-trail
to proceed at vP beyond Point 3,
[b] to execute a feathered stop at Point 5,
[c] to wait out its dwell time tD, and
finally for...
[d] the tail car of the train-in-trail to reach
Point
3'?
Exclamation Point Alert: For the base-case
values used in the Trail Braking puzzle, the
minimum headway imposed by a Station Stop
is more than 92 seconds, which is more than twice as long
as the headway at crusing speed along trackways and tunnels -- actually
independent
of cruise speed
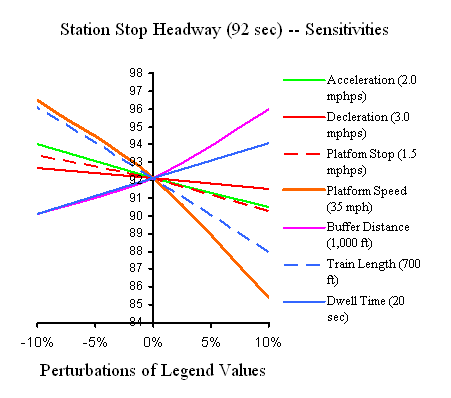 Accordingly,
a time-table for "a train a minute" is out of the question. The star-graph
on the right provides a sensitivity analysis, using 10% perturbations of
the base-case. Five observations: Accordingly,
a time-table for "a train a minute" is out of the question. The star-graph
on the right provides a sensitivity analysis, using 10% perturbations of
the base-case. Five observations:
-
Headway is most sensitive to Platform Operating Speed vP
--
in this case, faster is faster -- and may be improved best by the
application of platform doors, as seen on elevators and people-movers.
-
The feathered Platform Stop deserves design attention, particularly
if platform doors are applied to enable higher platform operating speeds.
-
Acceleration has a significant impact on headway, which confirms
an advantage of all-wheel, electric propulsion systems over locomotive-per-consist
trains (typically limited to < 1 mphps).
-
Buffer Distance depends on precision in service braking.
Using a value larger than that in the base-case should be avoided.
-
Parameters such as Train Length and Dwell Time
are not likely to be variable in a train control system design but are
included for completeness in the sensitivity analysis.
 As
we have discovered, cruise speed vC does not play
a part in determining minimum headway, which will be affected only by events
between Point 3 and Point 3'. Travel time between stations, on the
other hand, will be dominated by vC, as you will discover
when you try your hand at solving the Trip-Time
puzzle. As
we have discovered, cruise speed vC does not play
a part in determining minimum headway, which will be affected only by events
between Point 3 and Point 3'. Travel time between stations, on the
other hand, will be dominated by vC, as you will discover
when you try your hand at solving the Trip-Time
puzzle. |
 Trains,
planes, and automobiles – they all carry passengers, which necessitates
stopping from time to time. In railroading, headway is determined
by station stops.
Some people may be astonished to learn that headway has nothing to do with
"safe following distance" at crusing speed along trackways and tunnels.
The previous sentence deserves exclamatory punctuation, as we shall see.
Trains,
planes, and automobiles – they all carry passengers, which necessitates
stopping from time to time. In railroading, headway is determined
by station stops.
Some people may be astonished to learn that headway has nothing to do with
"safe following distance" at crusing speed along trackways and tunnels.
The previous sentence deserves exclamatory punctuation, as we shall see.

 Accordingly,
a time-table for "a train a minute" is out of the question. The star-graph
on the right provides a sensitivity analysis, using 10% perturbations of
the base-case. Five observations:
Accordingly,
a time-table for "a train a minute" is out of the question. The star-graph
on the right provides a sensitivity analysis, using 10% perturbations of
the base-case. Five observations:
 As
we have discovered, cruise speed vC does not play
a part in determining minimum headway, which will be affected only by events
between Point 3 and Point 3'. Travel time between stations, on the
other hand, will be dominated by vC, as you will discover
when you try your hand at solving the Trip-Time
puzzle.
As
we have discovered, cruise speed vC does not play
a part in determining minimum headway, which will be affected only by events
between Point 3 and Point 3'. Travel time between stations, on the
other hand, will be dominated by vC, as you will discover
when you try your hand at solving the Trip-Time
puzzle.