Sloping in the Dark
$Description: C:\G Drive\niquette\images\solution.gif$

Metaphorical Pun.
Copyright ©2004 by Paul Niquette, all rights reserved.

Will you be glad you did what the puzzle calls for?

Quite possibly not.

$Description: C:\G Drive\niquette\images\flam-f.gif$ inal approach to an airport calls for the pilot to maneuver the aircraft onto a flight path that is aligned with the runway centerline and slanting downward on a straight line called the "glide slope." The task is made decidedly more challenging at night -- especially at a remote airport with only runway lights for ground reference. The pilot must "connect the dots" (see illustrations) in order to synthesize a three-dimensional image of the runway beyond the windscreen while aiming for the "touch-down zone" at the threshold of the invisible pavement so as not to overshoot the landing.

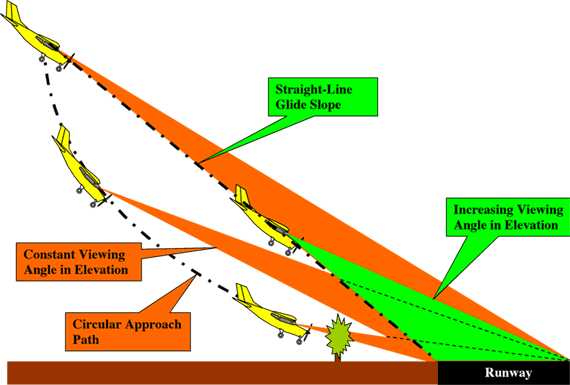
$Description: C:\G Drive\niquette\pictures\slopdk2.gif$ Inside the cockpit, the pilot controls the plane with the intention of maintaining a constant angle of descent. Meanwhile, the runway lights are gradually spreading apart and getting brighter. Their visual clues can be deceiving, as indicated in the diagram on the right.

It is tempting for the pilot to maintain a constant viewing angle of the runway. However, that policy produces one of aviation's more pernicious counter-intuitive results. The vertical approach path will not be a straight line but a curve -- the arc of a circle, in fact. The plane will descend below the straight-line glide slope. Approaching the ground, the pilot will necessarily have to apply sufficient power to keep from touching down short of the runway -- or worse.

$Description: C:\G Drive\niquette\images\flam-i.gif$ t was a clear and moonless night. On a flight to the Boulder City Airport in the 1960s, a certain private pilot found himself groping in the dark over sage and sand toward what was supposed to be a routine landing in the desert. He clicked his microphone key three times on the Unicom frequency, and the "pilot-operated" runway lights came on bright. The wind was calm. As the Cessna Skylane approached the ground on final approach, its pilot sat up proudly in his seat making minor pitch adjustments to establish a constant airspeed and changing throttle settings for maintaining a constant viewing angle of those runway lights. Ho-hum.

And then, and then...

The pilot that night was not thinking back to the 1940s and a certain geometry class and one homework problem. The assignment was to prove that a given chord on a circle subtends a constant angle as measured from any point on the circumference of the circle. The whole class groaned, of course. Nothing could be less meaningful to a teenager. Let us retrospectively apply geometry to the Sloping in the Dark puzzle.
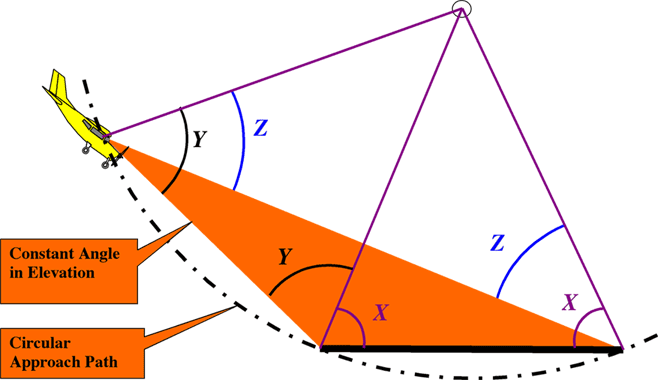
$Description: C:\G Drive\niquette\pictures\slopdk3.gif$
What the student sees here are three overlapping isosceles triangles, all sharing radii of the circle as their common sides and each having a chord of the circle as its uncommon side.

One of those chords represents the runway, and it is fixed. So is X, the angle appearing twice, once at each end of the runway. Angle X is subtended by radii of the circle. Another chord coincides with the pilot's view of the runway threshold, and Y appears twice, both times subtended by radii of the circle. Finally, a chord of the circle coincides with the pilot's view of the far end of the runway, with Z being the angle appearing twice between that chord and respective radii of the circle.

The angle that interested those geometry students back in the '40s and should have interested one of them in the '60s is Y - Z, the angle subtended by the runway itself. The angle Y - Z can be derived by taking a walk around the orange triangle adding up the angles as follows:

(X + Y) + (Y - Z) + (X - Z) = $Description: C:\G Drive\niquette\images\pi.gif$

Sophisticated solvers know that the three angles of any triangle always total $Description: C:\G Drive\niquette\images\pi.gif$ radians (180 degrees). With a little algebra, we find that...

(Y - Z) = ( $Description: C:\G Drive\niquette\images\pi.gif$ - 2X) / 2

...and since every term on the righthand side of the equation is constant, the angle Y - Z is constant, QED (quod erat demonstrandum "which was to be demonstrated"). Holding Y - Z constant results in an unwanted steepening of the approach. Bummer.

$Description: C:\G Drive\niquette\images\flam-o.gif$ h, right, that erstwhile-geometry-student-turned-neophyte-pilot-turned-aspiring-puzzler was more than astonished when the landing lights picked up the reflection of an "Airport" sign on the dirt road along the boundary of the airport. None too soon, as it turned out. The engine balked when full power was suddenly demanded, and with its flaps extended, the Skylane was quite reluctant to arrest the glide. Whew.

$Description: C:\G Drive\niquette\images\line.gif$

Epilog

A handful of non-pilot solvers have complained that they were misled by memories of their most recent happy-landing experiences characterized by the airliner gently pitching up just before touchdown.

The aviation term is "flare," and pilots generally postpone the maneuver until after at least the first pair of runway lights have disappeared below the windscreen -- a moment when the runway pavement is already well illuminated by the plane's landing lights.

Landings on aircraft carriers do not use much flare. Neither, apparently, do some of the world's airlines.

Black Hole Approach

$Description: C:\G Drive\niquette\pictures\runway.gif$ A popular expression for the Sloping in the Dark problem is "black hole approach." The resulting accident enjoys an official acronym CFIT (controlled flight into terrain). A number of lighting systems have been invented for preventing CFITs, including VASI (visual approach slope indicator), PAPI (precision approach path indicator), and, most notably for the author, HIRL (high-intensity runway lights). Then, in 2008, a friend sent me this picture...