Romance
in Numbers
Copyright © MCMXCVII by Paul Niquette. All
rights reserved.
|
mazing,
is it not, that Roman numerals have so many uses in the sciences despite
a functional obsolescence in the face of the 'positional notation' afforded
by Arabic numerals (see Prolix).
There prevails in Roman numerals an undeniable cumbersomeness, and yet
these ancient cyphers continue century after century to be printed on pages
and chiseled on stones.
Some benighted souls will dismiss the matter as mere
romance. Now really, does the word 'mere' ever belong in front of 'romance'?
The sophisticated solver of this puzzle
will recall that there are seven Roman symbols -- I, V, X, L, C, D, M,
standing, respectively, for 1, 5, 10, 50, 100, 500, 1,000 in the Arabic
numeral system. As fifth-graders used to be taught, you cannot simply read
a string of Roman numerals from left to right and translate them into Arabic.
There are rules to learn:
-
A symbol placed after another of equal or greater value adds
its value.
-
A symbol placed before one of greater value subtracts its
value.
Only certain combinations are permitted. Not all 49 possible
pairs of Roman numerals get applied: VV, LL, DD, for example, give way
to X, C, M.
The expression 'greater value' in the subtraction rule
is also limited -- you will not find VL or IL for 45 and 49, VC or IC for
95 and 99, VD or ID for 495 and 499, VM or IM for 995 and 999.
For their advocates, Roman numerals may provide a 'Roman
holiday' -- a time of enjoyment derived from the suffering of others.
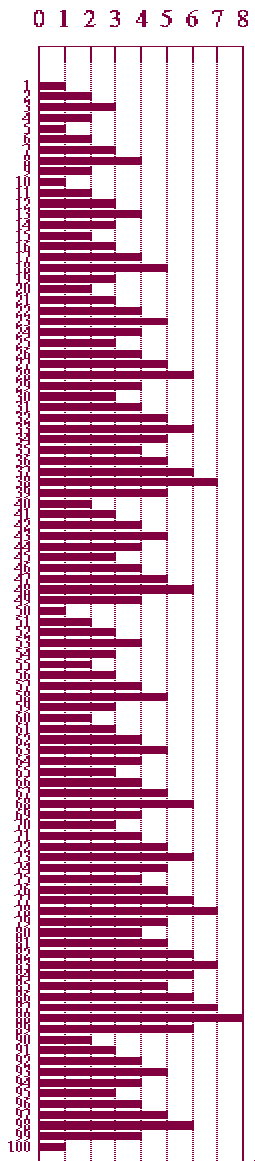
he
bars in the chart on the right represent the length in number of symbols
required to represent the corresponding Arabic number in Roman numerals.
In the range of one to a hundred, all but one of those numbers can be expressed
in Arabic with only two symbols. Observations...
-
The longest Roman numeral represents Arabic 88 with eight
symbols -- LXXXVIII.
-
Four require seven symbols -- 38, 78, 83, 87.
-
The most popular symbol is -- surprise -- X not I, with 150
versus 140 incidents.
-
The least popular, of course, is C, with 11 incidents between
one and a hundred.
-
Both V and L appeared 50 times each in the 100-count series.
A total of 401 symbols are required to enumerate 100
items -- twice the number that you would need using Arabic notation. Only
50% efficient, one might say. But hey, that's nothing. Try converting the
population of the world to Roman numerals:
5,123,456,789 would require 5,123,456 Ms followed by DCCLXXXIX.
Almost forgot: What year in
history required the largest number of Roman numerals to express?
Epilog:
For a puzzle that creates a new classification of numbers, see Reaman
Numeral.
