 The
Great Sonora Desert subsumes the Saguaro National Monument near Tuscon.
Vast and shadeless, the SNM ranks high among Arizona's natural wonders,
a cactus forest to prickle your mind. Spanish doesn't pronounce the g,
by the way: SA-WA'-RO. The
Great Sonora Desert subsumes the Saguaro National Monument near Tuscon.
Vast and shadeless, the SNM ranks high among Arizona's natural wonders,
a cactus forest to prickle your mind. Spanish doesn't pronounce the g,
by the way: SA-WA'-RO.
Elementary in its leafless form, almost Deco,
the Saguaro grows straight up from Earth, a pure green cylinder with ribs
and spines, hoarding moisture, standing stiff against the desert winds,
the obligatory focus for many a desert painting. The saguaro grows arms,
not branches. Each appendage juts out and immediately curves, forming an
elbow, then reaches perfectly skyward, parallel to the trunk, as if guided
by an internal static pendulum.
An opportunity to view thousands of saguaros may not enrapture
everyone. For me, it has sophisticated -- mathematical -- meaning. Each
of the saguaro's arms tends to emerge at an arbitrary level. But strangely
never at 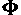 . The saguaro
refuses to abide by the Golden Section. . The saguaro
refuses to abide by the Golden Section.
The symbol 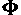 (phi,
usually pronounce FAE) is a
Greek letter, like (phi,
usually pronounce FAE) is a
Greek letter, like 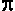 (pi,
usually pronounced PAE), commonly used
to denote the ratio of a circle's circumference to its diameter, and (pi,
usually pronounced PAE), commonly used
to denote the ratio of a circle's circumference to its diameter, and 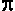 's
value, 3.14159..., thanks to computers, has grown in precision to over
10 million decimal places. Likewise, 's
value, 3.14159..., thanks to computers, has grown in precision to over
10 million decimal places. Likewise, 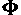 also
represents a ratio, called the "Golden Section." also
represents a ratio, called the "Golden Section."
To find 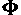 ,
start with the number 0 and the number 1. Add them together. You get 1.
Now add that 1 to the previous 1. This time you get 2. Are we going too
fast here? Now add the 2 to the immediately preceding 1, for a sum of 3.
So far, we have produced the following series of 'natural' numbers: 0,
1, 1, 2, 3. Continuing in like manner, adding the 3 we just computed to
the 2 from one step ago, and we get the next number in the series, 5. And
so forth, 8, 13, 21, 34, 55,... ,
start with the number 0 and the number 1. Add them together. You get 1.
Now add that 1 to the previous 1. This time you get 2. Are we going too
fast here? Now add the 2 to the immediately preceding 1, for a sum of 3.
So far, we have produced the following series of 'natural' numbers: 0,
1, 1, 2, 3. Continuing in like manner, adding the 3 we just computed to
the 2 from one step ago, and we get the next number in the series, 5. And
so forth, 8, 13, 21, 34, 55,...
|
0, 1, 1, 2, 3, 5, 8, 13, 21, 34,
55, ...
|
These numbers form the 'Fibonacci Sequence.' Its discovery
dates back to the early thirteenth century and to the most distinguished
mathematician of the Middle Ages, Leonardo Fibonacci, also known as Leonardo
of Pisa. He invented the first 'recursive number sequence.'
Over the centuries, countless mathematicians have devoted
their careers to the study of such integer sequences, discovering esoteric
properties in them. Philosophers have joined in the fun, writing recondite
monographs to one another about the mystical attributes of Fibonacci numbers.
Today's number theorists and computer scientists continue the arcane tradition.
As recently as 1962, a group of enthusiasts founded 'A Fibonacci Association'
-- in California, of course.
Fibonacci numbers grow big fast. The 41st entry in the series
amounts to more than 100 million. You can prove that for yourself in just
a few minutes.
In the mid-eighteenth century,
Robert Simson at the University of Glasgow discovered that the ratio of
two successive Fibonacci numbers "tends" toward a constant. Figuring this
out might have kept an old-time mathematician off the streets for weeks.
With today's massive computing power under our fingertips, we can effortlessly
reconfirm Simson's discovery in seconds. Actually, the proof is simple
{HyperNote 1}
Care to try? Take any Fibonacci number and divide it
by the next number in the series. Use 21 and 34. You get 0.61764705. Or
take the next pair, 34 and 55, which produces the ratio 0.618181818...
By the 29th and 30th number, you will see that the ratio has settled down
-- 'converged,' in math-talk -- so that you can perceive no change even
with many digits of precision. The ratio approaches the constant value
of...
Congratulations, you have found the value of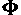 .
But why call it the "Golden Section"? And what does this have to do with
the saguaro? .
But why call it the "Golden Section"? And what does this have to do with
the saguaro?
Draw a line one unit long (by "unit"
can be meant an inch, a foot, or you can go metric if you like). Mark a
point on it. You now have two joined line segments. Call their respective
lengths 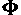 and 1 - and 1 - 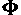 .
Now, let the point move along the line so that the following statement
applies: .
Now, let the point move along the line so that the following statement
applies:
The length of 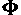 compared
to that of the whole line exactly matches the length 1 - compared
to that of the whole line exactly matches the length 1 - 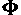 (the
part left over) compared to (the
part left over) compared to 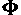 .
{HyperNote 2} .
{HyperNote 2}
The value of 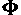 which
satisfies this relationship has received the name "ancient mean" and the
"extreme ratio." One finds the more colorful "Golden Section" used most
today. which
satisfies this relationship has received the name "ancient mean" and the
"extreme ratio." One finds the more colorful "Golden Section" used most
today.
For a line of, say, 100 centimeters, 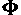 would
measure a little more than 61.8 centimeters, about 62% of the length of
your line. would
measure a little more than 61.8 centimeters, about 62% of the length of
your line.
Here ancient number theory and aesthetics strangely join.
If the 100 centimeters just mentioned represents the vertical side of a
piece of fine art, then the artist will position the focus of interest
about 62 centimeters from the bottom.
The viewer's eye will find that location most pleasing,
according to adherents of 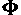 -losophy
(groan). -losophy
(groan).
The same theory influences the location side-to-side of artistic
emphasis. Thus do still-life artists place their baskets of fruit or flowers
at the Golden Section. Hah, that desert scene: Did you happen to notice
where the artist put the saguaro?
Look at the pictures around your room. Observe how often
this 'rule' has held.
-
That horizon-line in a seascape, for example. You can expect
to find it neither at the bottom of the canvas nor at the top -- not at
the center, either. Coerced by the Golden Section, the artist divides the
canvas with sky-above-ocean 62% of the distance from the bottom, and
-
foam in the foreground bursts upward, intersecting the horizon
62% of the way from left or right.
The frame-maker, too, appears to answer the call of 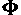 ,
imposing the 62% ratio, horizontal to vertical or vice versa. Ancient Greek
and Roman architects often designed their structures with the Golden Section
firmly in mind. ,
imposing the 62% ratio, horizontal to vertical or vice versa. Ancient Greek
and Roman architects often designed their structures with the Golden Section
firmly in mind.
See for yourself: Take calipers to the Parthenon.
Curiously, all the artists I know retch at numerical deliberations
such as those set forth above. Nevertheless, responding always to private
mental maunderings, they paint and carve 62% proportions upon canvas and
clay just the same.
In the dimensions of human face and figure, Golden Sections
preponderate. Check with that other Leonardo (da Vinci) on that. Some might
attribute such ratioing to Providential computations, others to Nature's
aesthetic intuition.
Which reminds me, mathematicians have classified 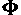 along
with along
with 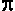 as an
"irrational number," an irrational choice of words for the case at hand,
seems to me. Irrational numbers, cannot result from the ratio of whole
'integers' -- Fibonacci numbers. as an
"irrational number," an irrational choice of words for the case at hand,
seems to me. Irrational numbers, cannot result from the ratio of whole
'integers' -- Fibonacci numbers.
The key to this paradox hides within that infinity business
in the derivation provided below.
-
Where parallel lines meet, so too do the rational and the
irrational.
-
-- Paul Niquette, 1997
|
But we must get back to the saguaro -- after just one more
observation about the Fibonacci Sequence. You will recall, we started
our series with the number 0. An especially appropriate selection and a
reminder of another debt of thanks we owe to Leonardo of Pisa. He first
noticed zero's magnificent properties and gave us 'positional notation,'
one of the greatest inventive leaps in history.
Think about it. Mankind needed the 'nul cipher' for its
ability to enable all manner of -- ta-dah! -- arithmetic. It was 0 that
the Romans didn't have. Consequently, their numerals have long ago resigned
themselves to non-arithmetic duties
-
(I) marking clock faces,
-
(II) performing unctuous service on cornerstones, and
-
(III) enumerating typographic lists.
For the Fibonacci series: after 0, we chose 1 -- unity --
which is just as fundamental as 0. These two ciphers, 0 and 1, comprise
the computer's 'binaries,' and with a string of fewer than a hundred of
them, one can count the number of protons and neutrons in the universe!
But I digress.
Whatever their historical significance to mankind, 0
and 1 have little influence upon on the Fibonacci Sequence, as it turns
out.
For no good reason, let's postulate a new family of Fibonacci
numbers, using exactly the same recursive procedure, but started with different
-- what shall we call them? -- "seeds." Try commencing your series with
a couple of numbers that did not arise on the previous list, such as 4
and 7.
Watch the entries grow: 11, 18, 29, 47,... Take out your
calculator and figure those ratios of succeeding values. They tend to the
same value, 0.618033988750! That Golden Section turns up again.
Experimentation with any number of seed numbers always shows
that outcome. Consider, too, the series started by 100 and 2. Notice how
fast the numbers grow. The 34th exceeds the population of the U.S.; the
40th, the population of the world. Yet, those ratios steadfastly approach
the same value 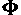 . .
You can plant a negative seed like -123 alongside, say,
77. After some vacillation, plus and minus, the numbers come out positive
and sail off to infinity -- at Simson's fixed ratio still. Another amazement:
By changing the 77 to 76, the consequent Fibonacci numbers stumble into
a black hole of unlimited negativity -- but the ratio 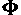 still
holds! still
holds!
 Such
a relentless 'emergent property' must have prevailed in many realms indeed.
Most often observed is that the relative sizes of successive chambers in
the nautilus obey ratio Such
a relentless 'emergent property' must have prevailed in many realms indeed.
Most often observed is that the relative sizes of successive chambers in
the nautilus obey ratio 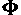 .
Look for Fibonacci sequences and therefore Golden Sections .
Look for Fibonacci sequences and therefore Golden Sections
-
in the spirals of sunflower heads,
-
in pine cones,
-
in leaf buds, and
-
in animal horns.
You find 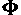 all
over the place. all
over the place.
Oh yes, and don't forget the elevation of the nominally
normal navel in proportion to the height of healthy humans (the belly button
of a 6-footer should be located almost exactly 44.5 inches above the floor).
 We
return at last to the saguaro. How astounding to observe that the saguaro,
standing sublimely upright against the Arizona sky, uniquely resists the
governance of the Golden Section! Unlike the sunflower and the pine, unlike
the nautilis and the ram, unlike the human -- especially unlike the human!
-- the saguara can defy We
return at last to the saguaro. How astounding to observe that the saguaro,
standing sublimely upright against the Arizona sky, uniquely resists the
governance of the Golden Section! Unlike the sunflower and the pine, unlike
the nautilis and the ram, unlike the human -- especially unlike the human!
-- the saguara can defy 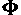 . .
Thus, we observe the eruption of the saguaro's arms at
an elevation never equal to 61.8033988750 % of the prickly trunk's height
(all data to the contrary should be disregarded).
As for the word prolix,
you can plainly see that the person who wrote these paragraphs has no use
for it.
Prolix adjective
-
Wordy and tedious.
-
Tending to speak or write at great length.
{Return}
|

{HyperNote
1} For more about Simson, see the solution
to Fibonacci Fantasy.
{HyperNote
2} You will find the derivation in the solution to Golden
Section. |
 The
Great Sonora Desert subsumes the Saguaro National Monument near Tuscon.
Vast and shadeless, the SNM ranks high among Arizona's natural wonders,
a cactus forest to prickle your mind. Spanish doesn't pronounce the g,
by the way: SA-WA'-RO.
The
Great Sonora Desert subsumes the Saguaro National Monument near Tuscon.
Vast and shadeless, the SNM ranks high among Arizona's natural wonders,
a cactus forest to prickle your mind. Spanish doesn't pronounce the g,
by the way: SA-WA'-RO.
 Such
a relentless 'emergent property' must have prevailed in many realms indeed.
Most often observed is that the relative sizes of successive chambers in
the nautilus obey ratio
Such
a relentless 'emergent property' must have prevailed in many realms indeed.
Most often observed is that the relative sizes of successive chambers in
the nautilus obey ratio  We
return at last to the saguaro. How astounding to observe that the saguaro,
standing sublimely upright against the Arizona sky, uniquely resists the
governance of the Golden Section! Unlike the sunflower and the pine, unlike
the nautilis and the ram, unlike the human -- especially unlike the human!
-- the saguara can defy
We
return at last to the saguaro. How astounding to observe that the saguaro,
standing sublimely upright against the Arizona sky, uniquely resists the
governance of the Golden Section! Unlike the sunflower and the pine, unlike
the nautilis and the ram, unlike the human -- especially unlike the human!
-- the saguara can defy