|
 Our initial proposals for
protecting Earth from a collision with Égaré at the Inbound Intersection turned
out to be unpromising.We
tried producing ∆V in both the prograde and retrograde
directions, only to learn that on Thursday July 21, 2022 the collision
is still likely. So much
for Tangential vectors.
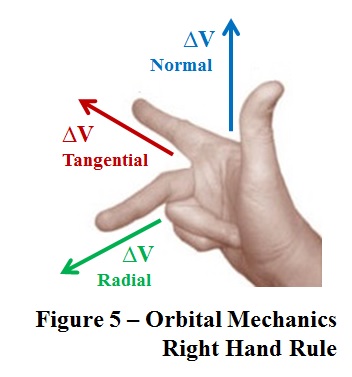
According to the 'right-hand rule' in Figure 5,
three choices for thrust vectoring are offered by
orbital mechanics to solvers. We have
examined one of them and made an original
discovery but were unsuccessful in
avoiding collisions between NEOs and our planet.
Let's see if either of the other choices offer a
solution to the Rock from the Sky puzzle.
Radial
Thrust Vectors
As shown in Figure
5, the Radial direction for a ∆V vector points
directly toward the sun ('radial-in') or away from
the sun ('radial-out'). The effect of a
radial-in ∆V is to rotate the whole orbital
plane in the prograde direction without changing
its shape or size. That case is
illustrated in Figure 6.
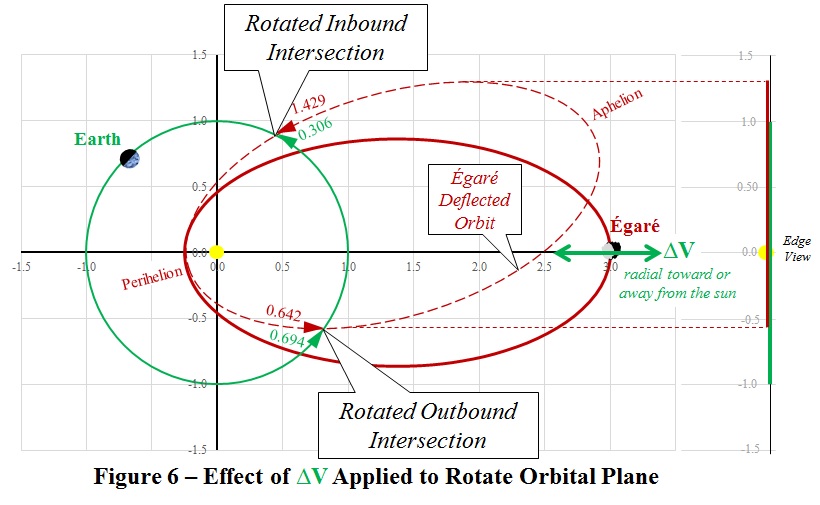 Also in Figure 6, we see that arrival
times at the Inbound Intersection for both Earth and Égaré are delayed, which tends to
cancel out the separation of their respective
arrival times for avoiding collision. This
case strongly resembles the discouraging
results in Figure 3. Likewise, the
effect of a radial-out ∆V is to rotate the whole orbital
plane in the retrograde direction without changing
its shape or size. That case strongly
resembles the results in Figure 4.
Normal
Thrust Vectors
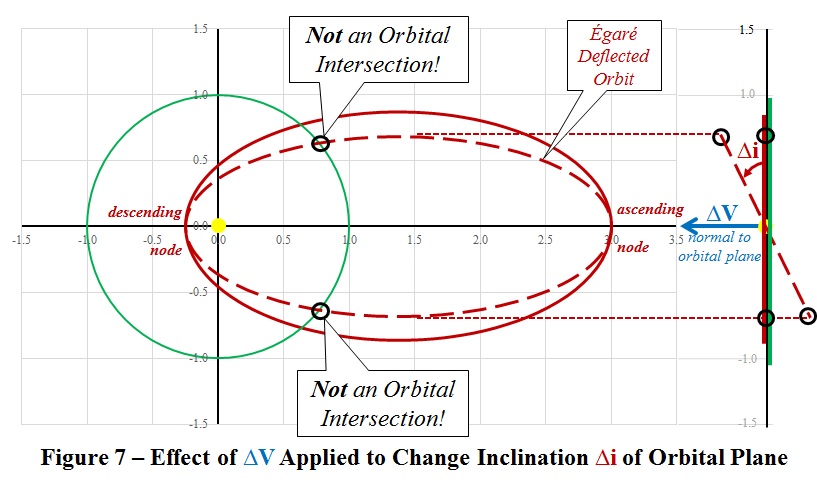
The two
non-pointing fingers of the right hand shown in
Figure 5, represent the orbital motion of Égaré. The Normal direction for a ∆V vector, indicated by the thumb,
points normal -- perpendicular -- to the orbital
plane and produces the effect shown on the right
side of Figure 7. In
particular, the orbital plane is tilted
along the major axis of the ellipse causing a
change in orbital
inclination ∆i.
Two orbital
elements used by astronomers are shown in
Figure 7. For the case depicted in the
sketch, the 'ascending node' passes through
aphelion. A ∆V vector in the other direction
(opposite to the thumb) will tilt the plane so
that the 'descending node' passes through
aphelion. Both cases offer an elegant
solution to the Rock
from the Sky puzzle...
The Égaré orbit with a non-zero
inclination does not intersect Earth's orbit. Ever!
Here then is our proposed solution...
|
Deploy and
maneuver a spacecraft capable of
delivering a massive payload for
station-keeping with asteroid Égaré, then apply its high
energy detonation to produce a vectored
thrust at aphelion to achieve a maximum
possible vectored thrust ∆V
normal to the
orbital plane in the direction that
assures an increase in whatever orbital
inclination
already exists.
|
...which is quite a
long sentence -- but only a beginning...
The Orbital Deflection puzzle
will continue to use asteroid Égaré as a basis for formulating a
mathematical model.
Puzzles with a Purpose will address
some of the immense challenges made necessary for
the protection of our planet from inevitable
threats by Near Earth Object (NEOs), including...
- Size of the NEO: Égaré was postulated to be 100 meters
in diameter. That is comparable to the
size of the asteroid responsible for the Tunguska
Event in 1908, which flattened 2,000 km2.
- Mass and Velocity: Assuming a
density of 5 gm/cm3, Égaré has a mass of
2.4×109 kg. At the orbital intersections the
velocity of Égaré is estimated to be
V = 39.4 km/s.
- Kinetic Energy: Asteroid Égaré will have a kinetic energy of 2.0
×109 kg-(km/s)2 at impact with planet Earth or 1,900×1015 Joules, equivalent to 450 megatons of TNT.
- Deflection Energy: A change in
orbital inclination of 1/10 degree for asteroid
Égaré requires as much as 173×109 Joules at aphelion where V = 6.7 km/s.
- Payload Mass: To deliver 173×109 Joules of energy to a
rendezvous with Égaré at aphelion requires a
spacecraft capable of lifting of tonnes of payload to
escape velocity.
- Delivery Distance: The aphelion for
Égaré is located at 3.0 EU = 450 Mkm from the sun.
More than a year must be allowed for delivery --
with gravity
assist, say, from Mars,
- Prediction Accuracy: The mission
demands extremes in precision, and line-of-sight
tracking is limited. The advanced
placement of a transponder
in orbit around Égaré will be necessary.
- Guidance for Thrust Vectoring: The transponder
satellite will also be used to gauge features
and tumbling motion on Égaré and to relay adjustments for
deployment of the deflection tools.
Epilog
In his commentary on the Trampoline Deorbiting
System my friend George McIlvaine added a
paragraph entitled "The problem of large rocks
falling from the sky." Here is an excerpt...
Every few years we
read about an astronomical near miss, usually
after the fact And the reports
always mention that not all the asteroids have
yet been identified. So
a sneaky pop-up asteroid intersecting Earth’s
orbit with little warning when Earth happens to
be at the intersection point has an estimated
probability that is not reassuring. Long
term identification and deflection is not 100%
effective, so are there other countermeasures?
That was the
inspiration for the Astrogating Asteroids
puzzle, in which one will find a minor
discovery...
In order for Earth to collide with a
non-coplanar NEO, the latus
rectum of the asteroid's orbit must
coincide with the diameter of Earth's orbit
along the line of orbital intersection.
...which seems to
grant immunity from orbital collisions to just
about any non-coplanar NEO.
That set off a
three-month web-based research effort leading to a
proposal for what may be a unique deflection
stratagem. It is informally presented in the
Rock from the Sky
puzzle and includes this surprise...
|
Discovery
Alert: A search of the
Internet by your puzzle-master has found
proposals for vectoring of ∆V only in
the tangential direction -- with
no acknowledgement of this catastrophic
phenomenon at the Inbound Intersection!
|
Solvers, your
comments are invited.
|
