Copyright ©1999 by Paul Niquette. All rights reserved |
|
Copyright ©1999 by Paul Niquette. All rights reserved |
|
x y y / z z x that approximates the value of pi to better than one part in 10 million.  t
is always possible to find a rational approximation for
an irrational number to any desired degree of precision.
For example,...
π ≈ 31,415,927 / 10,000,000, ...but that takes eight ciphers to express, hardly making it as Easy as Pi to remember. For the puzzle as stated, xyy / zzx, a reasonable assumption is that all three ciphers x, y, z are distinct from each other. We observe that none of the three ciphers can be zero.
To get a quotient greater than 3, x has to be at least 3. The smallest value for z is 1, which means that the smallest denominator of the fraction is 113. The fraction, then has the form 3yy/113. We break out our calculators and merely test appropriate values of y as follows:
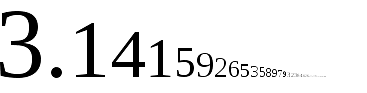
Back in the mid-twentieth century, a sophisticated solver had only a slide rule for arithmetic operations and was limited to three digits of accuracy. The value of π was often approximated as 22/7. Any modern calculator will show that 22/7 = 3.142857142857..., which is accurate to only about 4 parts in 10,000 or 0.04%. That same calculator will confirm that 355/113 = 3.141592920..., which differs from 3.141592654... by less than one part in 10 million or 0.0000085%. To put that precision in perspective, if the earth were a perfect sphere with a diameter of 8,000 miles, its circumference could be estimated, using = 355/113 with an error of no more than 11 feet 31/4 inches. {Return}
Making the Irrational Rational -- Almost The sophisticated solver knows how to use a spreadsheet to create an interactive 'model' of a problem. Here is one way to approximate any irrational number N by a rational number R, which is the ratio of two integers, call them Numerator and Denominator, which are 'mutually prime' (without common factors) to any specified degree of precision P. Spreadsheet conventions include
rows designated by numbers 1, 2... fixed or non-relative addressing requires a preceding $ arithmetic operators +, -, *, /, int logical operations if(condition, do this, else do that), min(range) Let A2 = P [for example P = 0.000001 means '1 part per million'] Let B1 = Numerator [arbitrary 'Seed': for example B1 = 1 (to be changed later)] Write B2 = B1+1, B3 = B2 +1,... B100 = B99 +1 [100 trial Numerators] Write C1 = int(B1 / A$1 + 0.5) [generates the first trial Denominator]
int( ) selects the integer part of a number, but watch out: int(2.1) = int(2.9) = 2. + 0.5 enable int( ) to 'round-off': int(2.4 + 0.5) = 2; int (2.5 + 0.5) = 3. for N =  and
B1 = 355, C1 = 113 (check it out)
Write D1 = B1 / C1, D2 = B2 / C2,... D100 = B100 / C100 [100 trial Rs] Write E1 = (A$1 - D1) / A$1,... E100 = (A$1 - D100) / A$1 [error function] Write F1 = if(A$2 - abs(E1) < A$2, B1, 99999)
A$2 - abs(E1) compares the error to specified precision P if the error < P, place the corresponding Numerator in F1 if the error >= P, place an arbitrarily large number in F1 Write F100 = if(A$2 - abs(E100) < A$2, B100, 99999)... Write A3 = min(F1..F100) Your computer automatically generates a batch of one hundred consecutive integer values for the Numerator and divides each one by an integer Denominator producing a ratio R and comparing it with the N.
The first time you see something other than 99999 in A3, hoo-hah! You then copy A3 into B1 and see the Denominator in C1. Of course you can use bigger batches, if you like. Good practice would give the columns labels, and you may want to compute the value of P from some more convenient representation, say, 'percent error' or 'parts per million.' Using this method and batches of 1000, a certain puzzle-master found the following solutions to one part in ten million in a matter of minutes:
{Return}
|
|
|
|
|
|
owever
irrational,