Nail-Biter Ballots -- Solution

Nail-Biter Ballots

he ballot box is quietly tumbling into obsolescence, displaced not by the newest technologies in voting machines nor by the World Wide Web but by the oldest of technologies: the mail-box. Some states have already accomplished the improvement. By de-synchronizing the voting process, voters don't have to wait in long lines. Then too, each voter, ballpoint-in-hand, can take plenty of quality time to study ballots and campaign literature -- and websites.

By mail-in ballot, members of the electorate can vote early -- weeks before traditional election campaigns are over. For candidates and campaigns, that creates yet another political segmentation. In addition to age, faith, gender, occupation, party, and schooling, a whole new demographic of early deciders must be targeted before any ballots get mailed out.

Long after election day, bags full of postmarked envelopes come tumbling into county offices for county counters to count, resulting in Nail-Biter Ballots. Here are salients of a real life drama as described in this puzzle.

Two weeks after election day (11/18), 612,000 votes had been counted, and barely 66.67% were in favor of the tax increase, which required a 2/3rds majority to win. However, there were still 9,800 votes left to count. According to a newspaper report a week later (11/25), the measure was declared to have passed, with 66.78% of the counted votes being "yes." What is the largest possible number of uncounted ballots?

Sophisticated solvers will do some parsing and likely make six observations:

From 11/18, we learn that 66.67% of the ballots counted at that time were in favor of the measure, a total of 408,020 (612,000 * 0.6667).
From 11/18, we learn that the total number of ballots cast, whether counted or not, was 621,800 (612,000 + 9,800).
From 11/25, we learn that the ballot measure was declared to have passed, so apparently not all of the 621,800 votes had been counted.
From 11/25, then, we must conclude that there remained an unknown number of ballots left to be counted. Let’s call them b_UNCOUNTED.
From 11/25, we learn that of the counted votes (621,800 – b_UNCOUNTED) 66.78% were in favor of the measure.
From 11/25, we learn that no matter how the remaining voters vote, the tax increase can be declared to have at least 66.67% of the total.

Thus, we can write…

(621,800 – b_UNCOUNTED) * 0.6678 > 621,800 * 0.6667
415,238 – 0.6678 * b_UNCOUNTED > 414,554
684 > 0.6678 * b_UNCOUNTED
1,024 > b_UNCOUNTED

…which means that b_UNCOUNTED = 0, 1, 2, … 1,023, the solution being...

1,023 Uncounted Ballots

Even if all 1,023 ballots were "no" votes, the tax measure would nevertheless receive 414,554 "yes" votes, just enough for passage.

Nota bene: This is not a statistical outcome tantamount to saying, "With ___% of ballots counted, we are confident in projecting that the measure will pass."

uppose that we let f_UNCOUNTEDrepresents the fraction of the total ballots cast that are uncounted at the intermediate (11/25) stage. Evidently b_UNCOUNTED= 621,800 * f_UNCOUNTED. One can re-write the expressions developed above as follows:

(621,800 – 621,800 * f_UNCOUNTED) * 0.6678 > 621,800 * 0.6667
(~~621,800~~ – ~~621,800~~ * f_UNCOUNTED) * 0.6678 > ~~621,800~~ * 0.6667
(1 - f_UNCOUNTED) * 0.6678 > 0.6667
1 - f_UNCOUNTED > 0.6667 / 0.6678
1 - 0.6667 / 0.6678 1 > f_UNCOUNTED
1 - f > 0.9983528
1 - 0.9983528 > f_UNCOUNTED
0.00164720 > f_UNCOUNTED
621,800 * f_UNCOUNTED < 1,024

Thus, with 99.83017% of the ballots counted and 66.78% of those voting "yes," one can declare absolutely that the measure will pass, winning at least 2/3rds of the total vote.

Sophisticated solvers might create a model from this solution. One simple way to do that is to use the expressions above as templates, thereby 'generalizing' from the 'particular'...

Particular General

(621,800 – f_UNCOUNTED * 621,800) * 0.6678
     > 621,800 * 0.6667 (b_TOTAL - f_UNCOUNTED * b_TOTAL) * f_{YES_VOTES}
     > b_TOTAL * f_{REQUIRED_TO_WIN}

(1 - f_UNCOUNTED ) * 0.6678
     > 0.6667 (1 - f_UNCOUNTED) * f_{YES_VOTES}
     > f_{REQUIRED_TO_WIN}

1 - f_UNCOUNTED
     > 0.6667 / 0.6678 1 - f_UNCOUNTED
     > f_{REQUIRED_TO_WIN/} / f_{YES_VOTES}

1 - 0.6667 / 0.6678 1
     > f_UNCOUNTED 1 - f_{REQUIRED_TO_WIN/} / f_{YES_VOTES}
     > f_UNCOUNTED

The model will declare winners if...
f_{YES_VOTES}
     > f_{REQUIRED_TO_WIN} / (1 - f_UNCOUNTED)

...to produce graphs like this one.

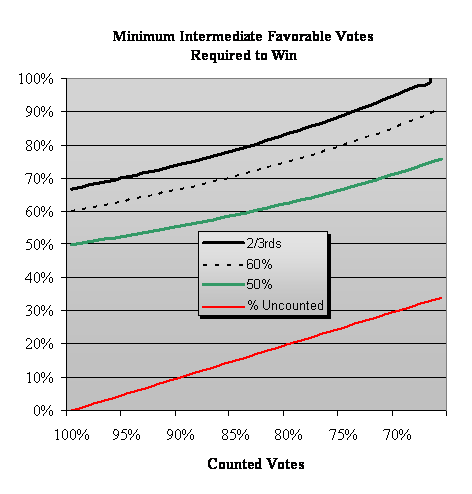On the far left, we see the California Nail-Biter Ballots case in which 99.83528% of the votes have been counted. The intermediate tally must be at least 66.78% in favor of the measure for the model to declare passage with a 2/3rds criterion (black curve). If, say, 15% of the votes remain to be counted, the intermediate tally must be 78% favorable for passage.

A measure or a candidate requiring a 50% majority can be declared the winner with only 75% of the votes counted, provided that the tally is at least 65% favorable (green curve).

Home Page

Puzzle Page

Math and Models

The Puzzle as a Literary Genre