Jump in a Lake

he statement in the puzzle, "You can drown in a lake the average depth of which is one foot" does not give a solver much information to work with. Many questions might go unanswered were it not for sophisticated instruments at our disposal called 'assumptions' (see Discovering Assumptions).

So for each unanswerable question ~~~ make an assumption:

Who are you? ~~~~~~~~ Someone who does not know how to swim.
How deep is the deepest point in the lake? ~~ Deeper than your height.
How tall are you? ~~~~~~~~~~~~~~~ Tall enough to be able to read.
Where is the deepest point in the lake? ~~~~~~~~~~~~~ In the middle.
What is the shape of the lake? ~~~~~~~~~~~~~~~~~~~~~~~ Circular.
What is the profile of the lake? ~~~~~~~~~~~~~~~ Sloping uniformly.
How big is the lake? ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Big.
How did you get into the water? ~~~ Someone in the boat said, "Jump in a Lake."

For sure, the sophisticated puzzle solver will come back and modify these assumptions to see which ones affect the outcome.

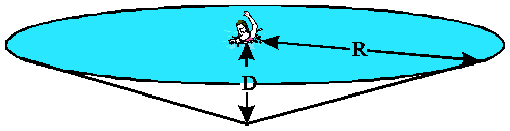
The Assumption Engine at Work

he resulting model of the matter is a cone-shaped lake with a non-swimmer thrashing around in the exact center. The average depth of a body of water can be obtained by dividing its volume by its surface area. The volume of a cone of radius R and depth D is given by

pi R²D / 3.

That's just one of those things sophisticated people know -- or else know how to find out.

Maybe you noticed that a cylinder with the same dimensions would hold three times the volume -- but maybe not. Anyway, a cylinder would have the same depth all over. Nobody would ever drown in a cylindrical lake the average depth of which is one foot.

Everybody knows how to calculate the area of a circle (pi R²). So the average depth, D_avg is given by...

D_avg= (pi R²D / 3) / (pi R²),
D_avg= D / 3 , and
D = 3 D_avg, but
D_avg= 1 foot; therefore,
D = 3 feet.

re you going to say it, or shall I? The disappearance of R in the equation means that the size of the lake does not matter. That takes care of assumption #6. But there's something else to get excited about, if you are so inclined. The deepest point in the lake is only...

...three feet.

You would have to be exceptionally short of stature or hopelessly clumsy to drown in that lake. That astonishing conclusion, we hasten to remind ourselves, results from the assumptions set forth above. Let's check them out.

How good are those assumptions?

A little research music, please...

The first assumption is the most critical. If you can swim at all, then you need a deeper lake so that the water is over your head within the radius corresponding to your maximum swimming distance. But the lake does not have to be deeper than your height in just the exact center; accordingly, we might consider modifying assumption #5 so that there is a flat space on the lake bottom forming a water-filled cylinder of depth D that you can just barely swim halfway across.

There is a name for that shape of lake, by the way, "frustum." {Definition}

Let that cylinder in the middle of the lake have a radius of R_swim. You may want to calculate the effect on D. If you do, expect something of a surprise -- that D is now less than three feet. Not only that but the lake gets shallower with increasing R_swim. The better you swim, the less you need to do so. Foozling with the rest of the assumptions won't change the outcome.

Accordingly, however valid the principle may be, the declaration I have been using for five decades (see, for example, A Certain Bicyclist) is not true.

How would you correct the metaphor, "You can drown in a lake the average depth of which is one foot"? You might try a cylinder within a cylinder, but be prepared for another surprise.

akes occur throughout much of the world, but they are most abundant in high latitudes and in mountain regions, particularly those that have been recently glaciated. They commonly occur along rivers with low gradients and wide flats and are associated with variations in the river channel. Many lakes are found in lowlands near the sea, especially in wet climates. That gives us some confidence in our assumption that lakes are shallower near their edges.

Lakes come in all sizes, but most have a surface area of about 100 square miles. Square miles? Lakes are not usually square, are they. A circular lake with a surface area of 100 square miles would have a diameter of about 11 miles. America has the world's largest freshwater lake in terms of surface area, but the Russians can claim the largest freshwater lake in terms of volume. If it were circular, Lake Superior, which covers almost 32,000 square miles, would be 200 miles across. Lake Baikal in Siberia holds 5,500 cubic miles of water. As a perfect cone 200 miles across, Lake Baikal would have an average depth of over 900 feet. How deep would it be at its center?

Lake Formation

More of the world's lakes have been produced by glacial action than in any other way, but given enough run-off from rivers and melting snow you can have a lake in any depression that has an outlet above the lowest point. "Water seeks its own level," people like to say. How does it learn what that level is? I wonder.

Factors in lake-making include...

barriers to drainage result in lake formation,
beach deposits across the mouth of a river,
alluvium laid down by a large river across the course of a smaller tributary, and
deltaic deposits that are laid down in a sluggish stream by a silt-laden stream may make a dam and produce a lake upstream.

he floodplains of rivers contain bodies of water called oxbow lakes, often with an island in the middle; they were formed in river channels that looped back upon themselves. Can't drown on an island. The craters of extinct or dormant volcanoes commonly contain lakes. Crater Lake in Oregon is one of the best known examples. Regions underlain by highly soluble limestone develop depressions known as sinkholes, which may fill with water under certain conditions to become lakes. The lake region of north-central Florida is of this type.

Lake Destruction

Viewed on the geological time scale, lakes are short-lived. Almost as soon as they are formed, three processes begin their destruction...

Inflowing streams carry sediment into a lake, thereby gradually filling the basin.
If the basin overflows, the resulting stream erodes a notch and thereby drains the depression.
The accumulation of organic deposits from vegetation may cause shallow lakes to become bogs or swamps and ultimately -- hey, dry land.

No danger of drowning there. {Return}

frustum n, pl frustums or frusta [NL, fr. L, piece] (1658): the basal part of a solid cone or pyramid formed by cutting off the top [or bottom] by a plane parallel to the base [in this case the surface of the lake, which is (ahem) horizontal]; also: the part of a solid intersected between two usually parallel planes. {Return}

-- Merriam-Webster's Collegiate Dictionary

Home Page Puzzle Page Logic and Reasonings The Puzzle as a Literary Genre