Natural Hypoteneese Solution

Natural Hypoteneese

he puzzle asks for the formula that generates a family of right triangles having the indicated Natural Hypoteneese starting with 3|4|5, 5|12|13, 7|24|25, 9|40|41. Two observations:

The smaller side is apparently any odd integer starting with 3. Let x = 2n +1.
The hypotenuse is one larger than the larger side. Thus, h = y + 1.

The challenge comes down to figuring out the value of y as a function of n. The expression "figuring out" ranges in meaning from foozling to formally deriving. In this case, some guessing, with the help of a spreadsheet, comes up with y = 4 n& (pronounced "n totorial," as introduced in Roulette's Frets). Since n& = n(n +1)/2, y = 2n(n+1). The solution, then, is given by...

x = 2n +1

y = 2n(n + 1)

h = y + 1

You might enjoy proving that these formulas work for all values of n...

[2n +1]² + [2n(n + 1)]² = [2n(n + 1) +1]²

You might also enjoy exploring the question of how many Natural Hypoteneese there are. Well, of course, there is an infinite number -- in each family. Still, there are plenty of integers that are not Natural Hypoteneese. The graph below shows the cumulative Natural Hypoteneese in relation to the natural numbers.

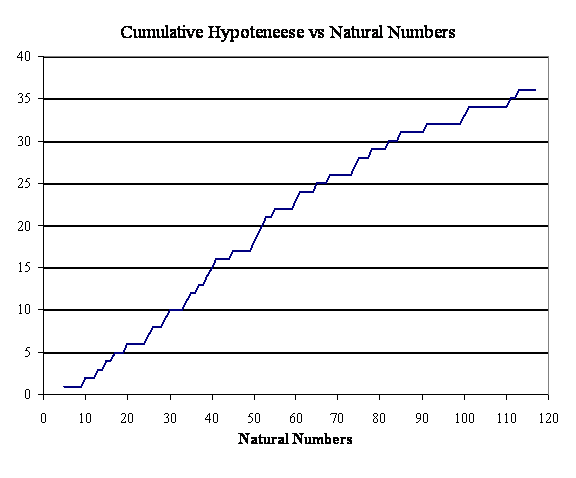
ur old friend the "three|four|five triangle" is the first triangle shown and has its natural hypotenuse placed in the lower left of the graph corresponding to natural number 5. The line rises gradually, going flat along the way indicating natural numbers that cannot qualify as Natural Hypoteneese. At natural number 55, we see an accumulation of 22 Natural Hypoteneese, for a ratio of 40%. That's as large as it gets! Excuse the exclamation point. At natural number 110, the ratio has fallen to 29%. What do you suppose the asymptote might be?

You are invited to send your favorite observations about Natural Hypoteneese here.

Home Page

Puzzle Page

Math and Models

The Puzzle as a Literary Genre