Natural Hypoteneese 
Word Origin
hypoteneese (n) plural of hypotenuse

Copyright ©2008 by Paul Niquette.  All rights reserved..

ack in some indefinitely early age, we have been taught the Pythagoras Theorem, "The square of the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides."  For more than 25 centuries, the Theorem has been learned and found useful.  Never mind that in modern times it has been misquoted in a popular film and lampooned in a world-class groaner. 

Just as famous in our scholastic youth was the "three|four|five triangle," wherein integers 3 and 4 provide the dimensions for the two sides and 5 represents the length of the hypotenuse.  Accordingly, the square of five (52 = 25) equals the square of three (32 = 9) plus the square of four (42 = 16). 

An unlimited number of triangles can each have 5 for their hypoteneese.  The square of their common hypotenuse 25 can be produced as the sum of 12 integer pairs... 
 

1 + 24 = 25 2 + 23 = 25 3 + 22 = 25
...
 12 + 13 = 25

The members of only one pair, 9+16=25, are both squares of integers.  The dimensions in other pairs are generally not integers, one or both will be irrational numbers formed as products, each pair including the square root of at least one prime integer...
 

1|2(2)1/2(3)1/2|5 (2)1/2|(23)1/2|5 (3)1/2|(2)1/2(11)1/2|5
...
 2(3)1/2|(13)1/2|5

In mathematics, positive integers are also called natural numbers.  For Natural Hypoteneese puzzle, we shall define a natural hypotenuse as an integer that can be formed as the square root of the sum of the squares of two integers.  The "three-four-five triangle" offers the smallest natural hypotenuse.  Don't you wonder how many other right triangles exist that have integers for all three sides?

epicted in the graph below are the dimensions of 15 triangles with Natural Hypoteneese plotted according to the lengths of their non-hypoteneese.  The "three|four|five triangle" sits in the lower left corner of the graph.  Some observations...

  • A straight line is clearly formed by integer multiples of the "three|four|five triangle."  Thus, we have 6|8|10, 9|12|15,...24|32|40... 
  • Note, there are an unlimited number of members in this family of Natural Hypoteneese.  Their dimensions are given by 3n|4n|5n| for n = 1, 2,...
  • The 8|15|17 triangle marks the beginning of another family of Natural Hypoteneese, formed as 8n|15n|17n.  The next member (n = 2) is shown on the graph as 16|30|34.
  • Likewise for 20|21|29, which begins another family of Natural Hypoteneese, with 20n|21n|29n, such that for n = 2, the triangle 40|42|58 lies outside the graph boundaries.

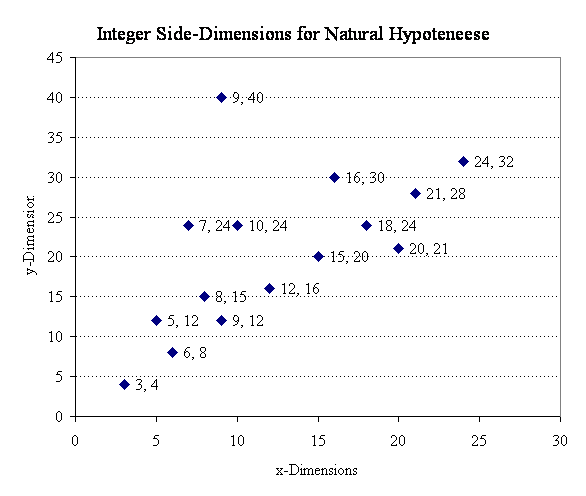
here is something interesting about the 5|12|13 triangle.  As with any triangle having a  natural hypotenuse, 5|12|13 is the first member on a straight line in the graph indicating a family of Natural Hypoteneese, each member being formed by multiples.  The graph shows 5n|12n|13n producing 10|24|26 for n = 2. 

The triangle 5|12|13 is also the second member of another whole family, which begins with our old friend the "three|four|five triangle."  This family of Natural Hypoteneese includes 7|24|25 and 9|40|41, which you will notice do not lie along a straight line in the graph.
 

What is the formula for the family of Natural Hypoteneese
that includes 5, 13, 25, 41?
. 
GO TO SOLUTION PAGE
Solution

Word Origin

Everybody knows (a) that hypotenuse means the side of a right triangle opposite the right angle and (b) that goose means a web-footed, long-necked, typically gregarious, migratory, aquatic bird -- so gregarious, apparently, that (c) goose has been awarded the word geese for its plural not gooses. 

Now, hypotenuse is not known for being gregarious, there being only one per right triangle.  In all of history, perhaps no occasion has arisen that called for the plural of hypotenuse. For this puzzle, solvers are invited to think of hypotenuses in groups or families, for which using the word hypoteneese seems appropriate.