Copyright ©2005 by Paul Niquette, all rights researved. |
|
Copyright ©2005 by Paul Niquette, all rights researved. |
  n
the right you see an animated figure called an
"epicycloid." It is
produced by a point on the circumference of a circle
rotating inside the
circumference of a larger circle without slipping.
The outside circle
has a radius a and the rotating circle
has a radius
b.
For the case you see here,
b = a/3, and the
figure in red is called a "deltoid."
Animation by Weisstein, Eric W. "Deltoid." From MathWorld -- A Wolfram Web Resource. |
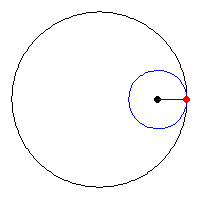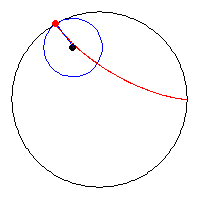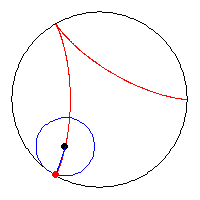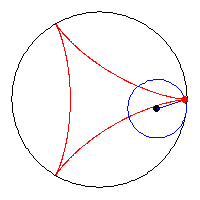
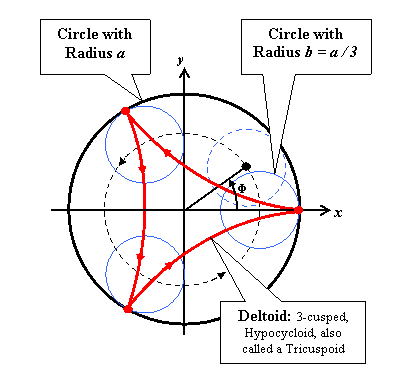 Examine
the
figure on the left. You will see that as the
inside circle rotates
clockwise it is orbiting counter-clockwise, while its
center makes the
angle
Φ
with
the x axis. Epicycloids are best
described mathematically
by writing a pair of equations using
Φ
as a parameter...
x = (a - b)
cos Φ
- b cos [(a - b) Φ/
b]
The radii a and b can take on any values. Integers produce closed figures. For the deltoid, b = a / 3, and for simplicity, we can let a = 3 so that b = 1. The equations then read as follows: x = 2 cos Φ
+ cos (2 Φ)
Perhaps you are asking the question, "What does all this trigonometric stuff have to do with sweeping a line segment around inside a figure as posed in the Circloid puzzle?" Read on. |
 n
the right, you see a point P on the deltoid produced by
the inside circle
having rolled so that its center makes an angle 
with the x axis. You also see
a point Q on the
deltoid produced by the inside circle having rolled on
around so that its
center makes an angle
+  radians with
the x axis.
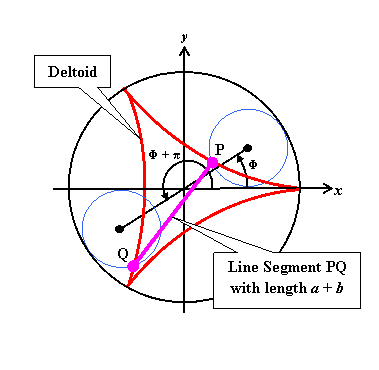Don't you now want to know what the length of the line segment PQ might be? Prepare yourself for a surprise. The equations for the deltoid tell us the exactly locations of P and Q as follows: xP
= 2 cos xQ
= 2 cos ( Trigonometry students know that cos ( xQ
= - 2 cos Φ
+ cos (2 Φ)
For calculating the length of PQ, we first take the following differences: xP
- xQ
= 2 cos Φ
+
cos (2 Φ)
+ 2 cos Φ
- cos (2 Φ)
= 4 cos Φ
...and applying Pythagoras Theorem, we find that... Length of PQ = [(xP - xQ)2 + (yP - yQ)2]1/2 = [16 cos2 (Φ) + 16 sin2(Φ)]1/2 = [16]1/2 = 4. Therefore, PQ = 4 units in
length. Notice, please,
that PQ = 4 no matter what that angle Φ
might be! Exclamation point intentional.
By inspection you
will see how the longest line segment that will fit
inside the deltoid
is indeed 4. So
the solution to the puzzle is...
Indeed, if b = a / (2k + 1) where k = 1, 2, 3..., then PQ will have the same properties no matter how large k gets to be. How about an exclamation point for that! The length of PQ will be given by [4k/(2k + 1)] a. Thus, as k increases without bound, the length of PQ approaches 2a. Hey, that's exactly the diameter of the outer circle. Which brings us all the way around to where the puzzle began. Our efforts have produced an epicycloid with an infinite number of cusps. If there is not a name for that, let's call it a circloid. Don't bother to look it up in a dictionary, circloid appears here first. |
 ome
puzzle-solvers may be disappointed that the Circloid
puzzle gives away the solution without showing how it
was found.
That may not be possible in this case. Here's
why. One day,
the author, who has an abiding interest in
lighter-than-air craft (see
"Sun
Ship"), launched
a search on the web that turned up a book entitled The
Deltoid Pumpkinseed.
That stimulated curiosity about the term "deltoid," and
a subsequent search
produced the Mathworld link you see above.
While watching that hypnotic animation, the author gradually became distracted by an irrelevant question: "What is the longest line segment that will fit inside a deltoid?" There was absolutely no reason to ask it. That idle query set off an investigation which resulted in a discovery. But the discovery was not the solution to a puzzle at all. Producing the Circloid puzzle was merely a matter of turning the discovery inside out. That left a huge gap in reasoning, though. Other puzzles have been created about the same way (see for example "Reaman Numeral" or "Fermat's Really Last Theorem") -- but the pathways to their solutions were gap free. So, then, what is the purpose of the Circloid puzzle? That will be found not in the success of one discovery but in the failure of another. 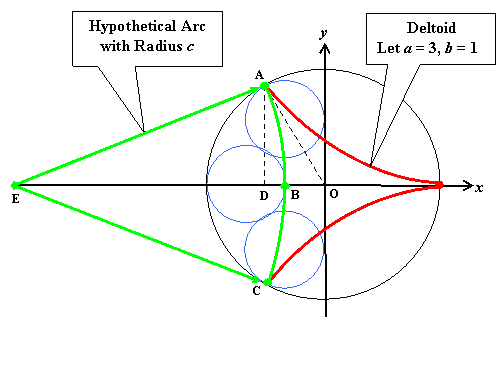 ake
a closer look at the deltoid. Does it not appear
to be made up of
three circular arcs? We can confirm that
hypothesis with a few mathematical
operations. If so, we may be on the brink of
another discovery here.
It takes only three points to define a circle, so let's
get started.
This diagram will help.
Hypothetical arc ABC is shown in green. Its unknown radius is... c = AE = BE = CE. By inspection, you will easily see that AO = 3, that BO = 3 - 2 = 1, and that angle DAO = 30o ( π/6 radians). Thus, DO = 3 sin( π/6) = 3/2. Now, BD = 3/2 - 1 = 1/2, which gives us right triangle ADE with hypotenuse c and legs (27/4)1/2 and c - 1/2. Pythagoras' Theorem and a little
algebra will do the rest:
c2
= [(27/4)1/2]2
+ (c - 1/2)2
=
27/4 + c2 -
c
+ 1/4, so that
|
|
|
|
|
|
