Fermat's Really Last Theorem

Copyright ©1997 by Paul Niquette. All rights reserved.
Sophisticated solver will see that there are really two questions posed in the puzzle. The first was unasked...
    What pair of numbers satisfy the equation x = yx/y?
That equation is not in an especially handy form. Kind of makes you want to get right in there and raise the whole thing to the yth power. If nothing else, that gives us all a nicer equation to gaze upon...
    xy = yx
...which has a quite pleasant symmetry, perhaps you will agree.

Old Pierre de Fermat would probably approve some experimenting around, like trying a few numbers. The technical term for the procedure is 'foozle.' Truth be known, that's how Pierre got to be known as the most productive mathematician in the 17th Century. Certainly, it was foozling that gave us Fermat's Last Theorem. {BackLink}

It does not take the sophisticated solver long to rule out 1 and 2, 2 and 3, 3 and 4. And then, suddenly, there's 2 and 4, so that 24 = 42. Zowie, the numbers 2 and 4 work. An exclamation point is optional.

Onward, sophisticated solvers. Onward to the main question...
 

There is only one pair of numbers
that will satisfy the equation
x = yx/y
Is this conjecture true?

A little more foozling and, golly, it does not look like any other pair of numbers will work. Hoo-hah for Fermat's Really Last Theorem. 

    But wait...
Exactly as specified in Fermat's Really Last Theorem, the values 2 and 4 are indeed a pair of numbers. They are something else, too -- integers. You might regard the previous sentence worthy of an exclamation point. I do. But I already used one for a sentence like that in Discovering Assumptons.
    One might reasonably suppose that if x were decreased a skoche and y increased a tad, the equation might still work. Accordingly, by the 'black letter law' of mathematicians -- which distinguishes 'number' from 'integer'-- Fermat's Really Last Theorem is doomed.
Just for fun (some people think math is fun, anyway), let's see if we can figure out a method for finding all the number pairs that satisfy the equation.
    In other words, we seek a mathematical expression that produces values for both x and y, such that x to the yth power equals y to the xth power.
Let y = kx. Why not? We're just having fun here.
    A sophisticated solver will regard k as a parameter.
The parametric form of the equation in Fermat's Really Last Theorem becomes...
    xkx = (kx)x  ~~~~~ by substitution,
    (xk)x = (kx)x  ~~~~~ by rearrangement,
    xk = kx ~~~~~~~~~~ after extracting the xth root, and
    xk-1 = k ~~~~~~~~~~~ after dividing by x.
We have derived a parametric expression for x...
    x = k[1/(k-1)] ~~~~~~ after extracting the (k-1)st root,
...and we can now derive a parametric expression for y...
y = kx ~~~~~~~~~~ by repetition of our starting point,
y = k * k[1/(k-1)] ~~~~~ by substitution, and
y = k[1 + 1/(k-1)] ~~~~~~~ by rearrangement.
So, where are we?

Looks like we can substitute any value for the parameter k and have returned to us the respective values for both x and y that satisfy the original equation. Might give that a hoo-hah, the sound of discovery.

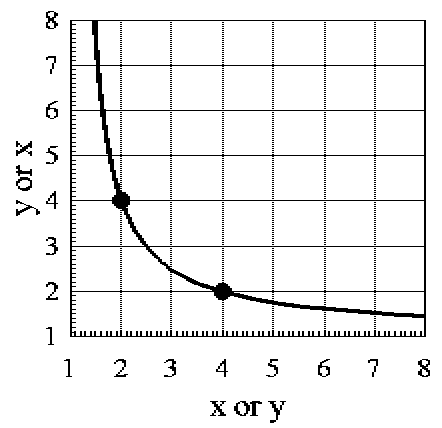
    The following table gives selected solutions, and the graph shows the locus of all the x-y pairs that satisfy the equation and thus disprove Fermat's Really Last Theorem.
x or y
1.411
1.463
1.530
1.624
1.765
2
2.478
3
4
5
6
7
8
9
y or x
9
8
7
6
5
4
3
2.478
2
1.765
1.624
1.530
1.463
1.411
Interchangeable Exponents

There is just this one other thing.

Had Fermat's Really Last Theorem used the word 'integers' instead of 'numbers,' as...
 

There is only one pair of integers
that will satisfy the equation
x = yx/y
Is this conjecture true?

...the conjecture would have been disproved anyway.

    Try x = -2 and y = -4.
Sorry about that, Pierre.

Epilog

More than five years after the publication of Fermat's Really Last Theorem, a cordial e-mail message was received from Peter Olsen, a colleague in Australia...
 
 

G'day, Paul,

Commenting on the theorem as posted...

x = y^(x/y)
...it struck me that with x = -2 and y = -4, substitution leads directly to...
-2 = -4^(-2/-4)
-2 = -4^1/2
-2 = 2i
...and I don't recall imaginary numbers fitting such equalities...

Is there an explanation for this apparent paradox?

Cheers,
Peter

are needs to be taken when manipulating formulas involving radicals such as z1/2. The notation is reserved either for the principal square root function, which is only defined for real z > 0, or for the principal branch of the complex square root function. Attempting to apply the calculation rules of the principal (real) square root function to manipulate the principal branch of the complex square root function will produce false results, like this...

-1 = (i)(i) = [(-1)1/2 (-1)1/2] = [(-1)(-1)]1/2 = [+1]1/2 = +1
To avoid making such mistakes when manipulating complex numbers, a strategy is never to use a negative number as a radicand, as for example (-z)1/2. Instead of expressions like that, one should write i (z)1/2, which is the intended use for the imaginary unit i.

Finally, using the original formulation of Fermat's Really Last Theorem, x = yx/y , a paradox arises even without using the imaginary unit i, for we see that substituting x = -4 and y = -2 leads directly to...

-4 = -2-4/-2
-4 = -22
-4 = +4
...which sure enough conflicts with the algebraic equivalent, xy = yx, for x = -4 and y = -2...
-4-2 = -2-4
1/(-4)2 = 1/(-2)4
1/16 = 1/16
Lurking in hidden assumptions about exponents are anomalies to the nth power.  For another example, have a look at those in the solution to Double Integrity. 


Home Page
Puzzle Page
Math and Models
The Puzzle as a Literary Genre