|
Copyright ©2009 by Paul Niquette. All rights reserved. |
|
The difference, 6 knots, would seem to
be the speed of the wind faced by the flight but not
necessarily the solution to the Wind
Circle puzzle. For that we must take
into account crosswind as well as headwind.
As a vector, wind has direction as well as
magnitude. The puzzle
did not provide enough information to determine wind
direction. Or did it?
A headwind facing any given course would of course be a tailwind enjoyed by the reverse course. The return trip over the same leg might be expected to take 8 minutes less time. Winds tend to be steady, changing only gradually. Reversing a wind's direction within a day is unlikely. An explanation that seems reasonable is that the wind aloft at the cruise altitude is perpendicular to the course of the two flights over the common route in both directions. The aircraft's Ground Speed vG is a vector aligned with the course for the flight, and the Wind Speed vW is a vector perpendicular to the course, together forming a right triangle with the aircraft's Airspeed vA as the hypotenuse. By the Theorem of Pythagoras... vW2 = vA2 - vG2...which, when solved for vW, gives us the solution to the Wind Circle puzzle. |
|
The Airbus must be flying its course directly across a jet stream, which can reach speeds of over 200 knots. We have solved the puzzle but we have not explained the title "Wind Circle."
Indeed, the pilot
has deliberately 'taken up' a heading to the left of
course by a 'Wind Correction Angle' aA. The resultant flight vector
is indicated as vG. Unlike the wind vector in
the puzzle, the red arrow is not perpendicular to the green arrow. In the depicted case, the
wind vector vW is acting at an angle aW to the Ground Track. We see
two components: a crosswind and a headwind,
such that vG < vA.
General 'wind triangle' calculations apply the following equations: Wind Correction Angle........ aA = arc sin (vW sin aW)...wherein the independent variables are vW and aW (The wind bloweth where it listeth). Holding wind speed vW constant, one can ascertain the effect of wind direction aW on ground speed vG. Generalizing still further, sophisticated solvers will probably want to represent windspeed and groundspeed as percentages of Airspeed vA... Ground Speed: [100%] vG / vA = [100%] cos aA - [100%] (vW / vA) cos aWMight as well be systematic about the investigation and generate a complete Wind Circle for all possible wind angles, thereby producing a graph like this... 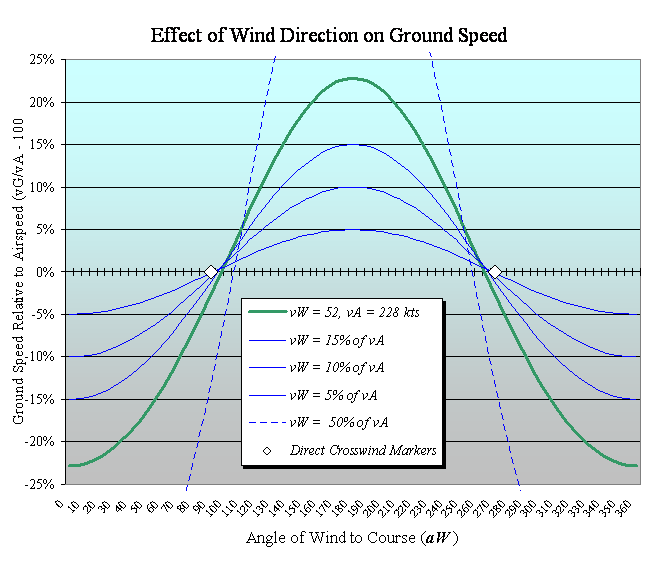
Finally,
remembering to keep time in
the numerator, the sophisticated solver will
find that for a round trip between
waypoints, the overall average ground speed will
range from 223 Kts down to 216 Kts depending on the
wind direction aW. |
 This picture shows Airspeed as a
vector vA retrospectively
superimposed upon the contrails of an aircraft
flying at cruise altitude. The red arrow indicates that a wind vector vW in that region of the sky is acting
on the flight causing the aircraft to be blown to
the right. An observer standing on the ground
would see the aircraft following a Ground Track to
the right of its heading as represented by the green arrow. In that direction lies the
flight's intended destination.
This picture shows Airspeed as a
vector vA retrospectively
superimposed upon the contrails of an aircraft
flying at cruise altitude. The red arrow indicates that a wind vector vW in that region of the sky is acting
on the flight causing the aircraft to be blown to
the right. An observer standing on the ground
would see the aircraft following a Ground Track to
the right of its heading as represented by the green arrow. In that direction lies the
flight's intended destination. 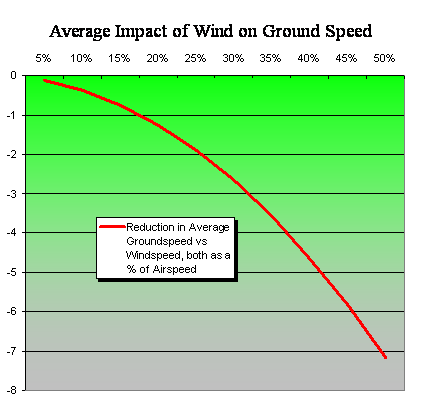 We
also see from the Wind Circle
above that, indeed, "on the average" (with the wind
blowing from any arbitrary direction), more often than
not, ground speed is less than
airspeed. The dashed blue curve shows an extreme
case, with vW = 50% of vA, such
that headwind components are in effect for
210 degrees -- 58% of the full Wind Circle.
We
also see from the Wind Circle
above that, indeed, "on the average" (with the wind
blowing from any arbitrary direction), more often than
not, ground speed is less than
airspeed. The dashed blue curve shows an extreme
case, with vW = 50% of vA, such
that headwind components are in effect for
210 degrees -- 58% of the full Wind Circle.