A cylindrical container with diameter D inches and height H inches requires a surface area...

[1]     A =  D H + 2 (/4) D ² square inches of material to accommodate a volume...
[2]     V = (/4) D ² H cubic inches. 

To facilitate the analysis, let us define a dimensionless ratio...

[3]     C = H / D, so that substitution of  H = C D into [2]...
[4]     V = (/4) C D ³ cubic inches, which we solve for D...
[5]     D = (4V / C) ^1/3 inches.

Substituting [5] into [1], produces the following relationship:

[6]     A = ^1/3(4V) ^2/3 (C + ¹/2)C ^-2/3  in which we identify two factors...
[7]     F_SIZE = ^1/3(4V) ^2/3 and...
[8]     F_SHAPE = (C + ¹/2)C ^-2/3 such that...
[9]     A =  F_SIZE F_SHAPE .

Observe that the size factor F_SIZE imposes the Square-Cube Law as follows:
 

Meanwhile, the shape factor F_SHAPE plays an independent role...
 

ur economic objective calls for the minimum value of A; however, F_SIZE is fixed by the assumed value of V in [2].  Thus, for the solution to Tin-Can Mystery puzzle, we must ascertain the value of C that produces the minimum value of F_SHAPE and compare it to 1.5.  Sophisticated solvers will remember their elementary Differential Calculus and proceed as follows:

[10]     d[(C + ¹/2) C ^-2/3] / dC = (¹/3)(C ^-2/3 - C ^-5/3) = 0, which simplifies to...
[11]     C ^-2/3  = C ^-5/3, and the only solution for that form is...
[12]     C = 1.0, which solves the Tin-Can Mystery puzzle...
 

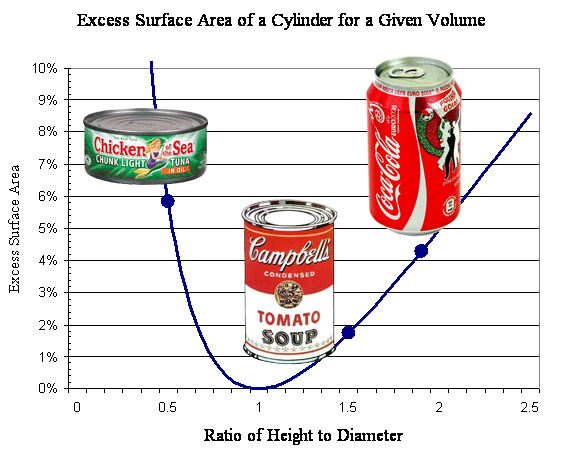
That will not surprise sophisticated solvers who know that for any volume, a sphere has the smallest surface area.  A tin-can with C = 1.0 mandates that H = D, which is about as close to a spherical shape as a cylinder can get.  For maximizing volumetric efficiency, designers of internal combustion engines exploit H = D (stroke = bore) in what they called the "square cylinder," by which swept area and therefore heat-loss is minimized for a given displacement.

Substituting [12] into [6], we obtain the minimum surface area for a cylindrical container required to accommodate a given volume...

[13]     A_MINIMUM =^1/3(4V) ^2/3 (1.0 + ¹/2) 1.0 ^-2/3 = ^1/3 (4V) ^2/3 (1¹/2).

Any value of C > 1.0 or C < 1.0 will require more than the minimum amount of material...

[14]      A_EXCESS = ^1/3(4V) ^2/3 [(C + ¹/2) C ^-2/3 - 1¹/2], as shown as a percentage of A_MINIMUM in the graph below...

hether the product of natural selection or intelligent design, size is not the only determinant of shape.  In the Tin-Can Mystery puzzle, the oil barrel accommodates more than 500 times the volume of a soup can but has the same shape (C = 1.5).  According to the graph, both will take about 2% excess material over the minimum for an enclosed cylinder. 

• Though consumed by the millions, few petroleum products are actually delivered in barrels. Those that do often take up floor space at points of use.  Reducing footprint makes sense. 

• Soup cans are indeed manufactured by the millions, with circumferential seams deliberately fashioned for opening by kitchen utensils, thus favoring smaller diameters.

• Other canned products require smaller packages but have a matching diameter to allow use of the same can-openers. With C = 0.5, say, they require 6% excess material (see graph).

• As shown in the graph, aluminum softdrinks have 'pop-tops'.  For them, C = 1.9, which requires more than 4% excess material.  What is the rationale for that?

Cupboards and refrigerators, boxes and box-cars, trailers and trucks, cartons and crates, warehouses and shipping containers -- all are rectangular in both elevation and planform, none are themselves cylindrical.  Cylinders are indeed round pegs in square holes.  It is easy to show that every can-in-a-box takes up 21.46% more volume than it holds (1- /4).  Not much can be done about that.  Intelligent design of the box or carton may be another story.

Let a box enclose cylindrical containers (cans) having dimensions D and C D.  Assume the cans are arranged in m by n rows.  The internal surface area of the box to accommodate the cans would be given by...

[15]     A_CANS = 2 D² [C (m + n) + m n].

Of course, the box will require more material than that for structure and strength. 

ou might enjoy reverse engineering the following real-life case: A take-home cardboard carton is designed to hold 12 aluminum softdrink cans in two rows of 6.   Each takes up a volume inside the carton V = C D³.  Unfold the carton and you will find a narrow flap for gluing along one of the long edges (m D), plus 100% glued overlaps on both ends (2 n D H). 

Try substituting these numbers into [15].  You will find the value of C that requires the least amount of cardboard is 1.9.  Coincidence? 

Epilog

The following explanation was received in July 2008 from Myles Buckley:

The 4% excess material is a function of burst strength vs crush load resistance, according to Duncan Hosford in "The Aluminum Beverage Can" in the September 1994 edition of Scientific American Magazine.  Hosford described the efforts of Coca Cola and Pepsi Co. to minimize the need for aluminium, which imposes by far the single highest cost of production for their canned soft drinks. 

The pop-can is very thin on its side-wall.  More aluminum by mass is found in the top ridges (not to cut the drinker's lips) and more again at the base.  The can has three "pieces." A slug of aluminum is extruded to form the base and sides; a disk forms the top (including the "button" that holds the pull tab); the pull-tab itself is the third piece.

As a cylindrical container, its aluminum sidewalls are afforded crush resistance by the pressurized contents.  The bottom is made burst resistant by the local mass of aluminium and strengthened by its annular shape designed for upright stability. 

Based on the engineering of modern aluminum -- not tin -- cans, I'd say that C = 1.9 is close to the ideal ratio for delivering soft drinks under moderate pressure. 

Same for beer, presumably.
-- PN