Let us conduct our analysis in the power domain using simplified parameters for a vehicle traveling at v mph...

Power to overcome aerodynamic drag = a v³
Power to overcome rolling and drive-train resistance = b v
Power supplied to accessories = c

a hp/mph³ is a coefficient relating wind resistance to power
b hp/mph relates constant rolling resistance to power
c hp represents power for accessories
v mph denotes instantaneous vehicle velocity

p[v] = a v³ + b v  + c

{1}      p[150] = 150³ a + 150 b + c = 300
{2}      p[60] =  60³ a + 60 b  + c = ?
{3}      p[0] = 0³ a + 0 b + c = 5
{4}      60³ a = (60%) p[60]

...and take note that there are four unknowns: a, b, c, and p[60].  It is not generally practical to make direct measurements of p[60] in a moving automobile.  Solvers have been given only this:  "At a 'highway speed' of, say, 60 mph, the Stingray's sleek design demanded a mere fraction of the engine's power, the rest being held in reserve for rapid acceleration."

Solving these four equations simultaneously gives the following values:

a = 0.0000823 hp/mph³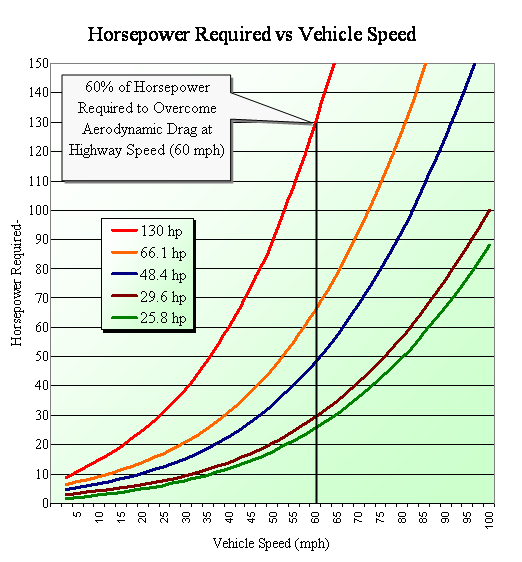
b = 0.114 hp/mph
c = 5 hp
p[60] = 29.6 hp

For calculating mileage, the puzzle invited solvers to assume an ideal Specific Horsepower of 2.0 hp/lb/hr.  A gallon of gasoline weighs 6 lb, which means that for every gallon-per-hour consumed gph, the engine will deliver 12 hp. By simply dividing delivered hp by 12, we obtain the fuel flow rate in gph.  Traveling at v mph, the vehicle consumes 1/12 gpm for each hp being demanded.  By dividing gpm into mph we get what we want, mpg...

...and our solution to the puzzle...
 

ou are invited to adopt the expression "60-60 AME" (aerodynamic mileage estimate) to describe the solution.  Thus, our 60-60 AME for 1966 Corvette is 23 mpg. The main assumption in the 60-60 AME is that, at 60 mph (highway speed), 60% of engine power for a given vehicle is devoted to overcoming aerodynamic drag. The validity of that assumption holds up for a wide range of vehicle shapes and sizes.  Here's why. 

Whereas the solution to the Look-at-Me Car puzzle has so far been conducted entirely in the power domain (hp), both aerodynamic drag and rolling resistance are customarily treated as forces (in lb or any other convenient unit described in Erg and Ugh).  We might write...

f[v] = a' v² + b' 

a' lb/mph² is a parameter relating wind resistance (aerodynamic drag) to speed
b' lb is a parameter that represents rolling resistance, independent of speed.

The rolling resistance parameter b'  is not a function of shape but varies directly with the vehicle weight (in particular the 'normal' force against the roadway).  That force, of course, is supported by the wheels at their respective 'contact patches', which are four finite areas defined mostly by wheel diameter and tread-width.  Thus, b'  also varies according as the two-thirds power of vehicle weight (w^2/3).  Exclamation point optional.

Using K_a and K_b for elementary constants of proportionality, the following relationships apply to a vehicle of a given shape, relevant to size, 

a' = K_a w^2/3 and b' = K_b w^2/3
a' / K_a  = b' / K_b
a' / b'  = K_a  / K_b = 1/ K
b'  = K  a' 

f[v] = a' v² + b' 
f[v] = a' v² + K a' 
f[v] v = a'  v³ + K a' v , but 
p[v] = a' v³ +K a'  v  + c.

p[60] =  60³ a + 60 K a  + 5
60³ a = (60%) p[60]

a = (40% p[60] - 5) / 60
b = K a

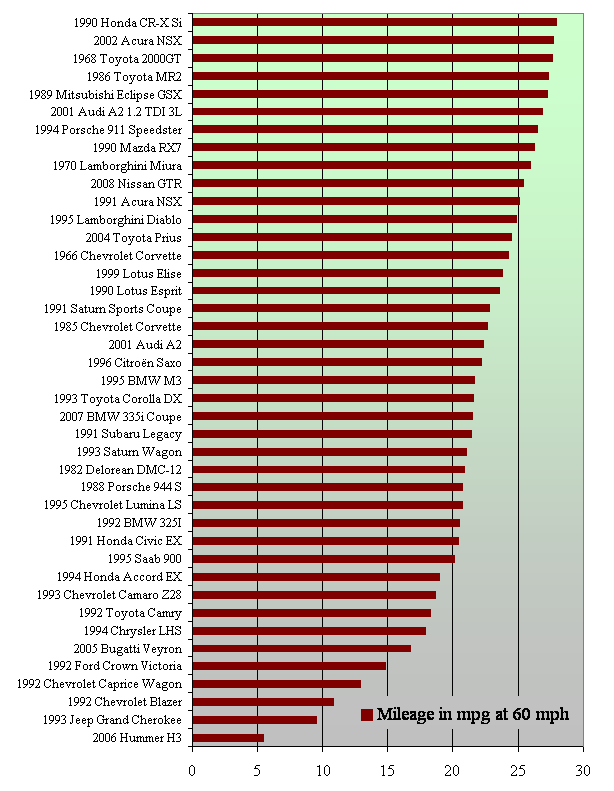To find the maximum for 12 v / p[v] = 12 v / (a v³ + b v  + c), set the first derivative to zero...

d{12 v / p[v]}/dv = d{12 v / (a v³ + b v  + c)}/dv = 0;
{12 (a v³ + b v  + c) - 12 v (3 a v² + b)}/{a v³ + b v  + c}²  = 0;
(a v³ + b v  + c) - v (3 a v² + b) = 0;
- 2 a v³ + c = 0.

Finally, as pointed out in To Brake or Not to Brake, mileage ratings for automobies... 

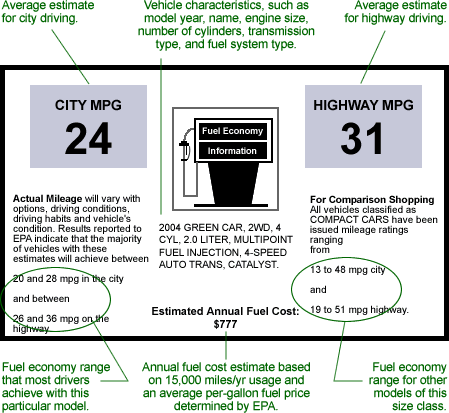
...are empirically determined by an EPA driver following a script on a dynamometer.  That these will be typically more generous than the steady-speed 60-60 AMEs is explainable by the low-speed segments of both the "Federal Urban Cycle" and the "Federal Highway Cycle."