Randomly Wrong

Copyright ©1999 by Paul Niquette. All rights reserved.
Often probability predictions are surprising. In the case of the coin-tossing experiment described in the puzzle, Dr. Theodore P. Hill of the Georgia Institute of Technology wrote in American Scientist, a "quite involved calculation" revealed a surprising probability. It showed, he said, that the overwhelming odds are that...
 
...in a series of 200 tosses, either heads or tails will come up six or more times in a row. 

Most fakers don't know this and avoid guessing long runs of heads or tails, which they mistakenly assume to be improbable. At just a glance, Dr. Hill can see whether or not a student's 200 coin-toss results contain a run of six heads or tails.  If they don't, the student is branded a fake.

To confirm Dr. Hill's probabilities relevant to coin-tossing, you are invited to review Randomly Right: the Mathematics and Randomly Right: the Model. To explore the psychology of cheating, have a look at Randomly Wrong: the Fakery.

Randomly Wrong: The Fakery

ow often are you invited by your instructor to cheat?  Let's say, you have decided to accept Dr. Hill's alternative not to flip a coin 200 times and record the results but instead "merely to pretend to flip a coin and fake 200 results."  You are determined to simulate the tossing of a coin.  That should be easy enough.  You know how an honest coin behaves.   So you press "Caps Lock" and start typing H's and T's at random across the screen.  What could be easier than that?

The sketch on the right depicts what is called a "state diagram."  At any given toss, your simulated coin will be showing either H or T and each arrow represents the probability for the face that will come up on the next toss.  "The coin has no memory," you remind yourself.  At every toss, it does not matter which side comes up, it is equally likely that the next toss will come up the same or opposite.  That's probability theory.

You might label the arrows p(H|H), p(H|T), p(T|T), p(T|H).  For the honest coin, of course, you know that...

p(H|H) = p(H|T) = p(T|T) = p(T|H) = 1/2.
While you are typing, a thought strikes you: "Even a dishonest coin has no memory."  Thus, for a bent or weighted coin that favors heads, you might expect...
p(H|H) = p(T|H) > p(H|T) = p(T|T)
...for which the symptom would be more H's than T's.  You have no intention of simulating a dishonest coin, so you keep track of the totals of H's and T's as you go along and try to keep them equal without being too obvious about it.  To fake randomness, you dare not type any kind of repeating pattern.  Faking is not as easy as you thought, is it?  And there's more...

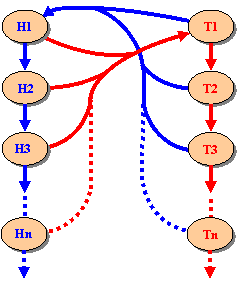At some point you look at what you have just typed and see a string of, say, two H's. In the course of your faked random typing you have arrived at state H2. This state diagram shows you the situation.  Here again, every arrow represents a probability.  You know that for an honest coin...

p(H2|H3) = p(H2|T1) = 1/2
Now, along comes a disembodied voice that whispers a question in your ear, "You have just typed two H's, do you want to show three H's in a row?"  You shrug and command your fingers to continue typing at what you intend to be random.  Maybe a T appears.  If so, fine.  Maybe instead, you look at your screen and see another H, which means you have arrived at state H3, such that the following probabilities are supposed to apply...
p(H3|H4) = p(H3|T1) = 1/2
...but the voice asks, "You have just typed three H's, do you really want to show four H's in a row?"  You try to disregard the question, probably with success.  Nevertheless, at some state, Hn, the voice will be so insistent that you find yourself tempted to favor typing a T, thereby struggling to simulate random -- but equal -- likelihoods for H's and T's.  According to the puzzle solution above, that temptation apparently becomes so strong that n < 6.  States H6 or a T6 simply do not arise in faked coin tosses.

The psychology explored in the the Randomly Wrong puzzle is elementary and relevant to gambling. Whereas the coin has no memory, you do.  You must try to keep in mind that wheels and dice have no memory.   Wagering selections call for anticipating an outcome based on probabilities, which is tantamount to faking random events.  Listening to that voice can lead to your downfall.  Instead, when you observe some repeating pattern, like six H's, you might try to visualize that somewhere else in the universe, six T's in a row have just shown up.

You may have noticed that psychology takes us out of pure probability theory and into the realm of statistics.  Computers are sensational for analyzing statistical phenomena (see, for example, Randomly Right: the Model).  The faking of random coin tosses by real people offers an opportunity to discern any number of psychological insights.  Consider the development of a Fake Randomizing Skill Database having the objective to calibrate the cognitive simulation of randomness, characterized by...

Cheating, of course, will have to be re-defined to mean the use of a random element.

Finally, for representing faked coin tosses, the arrows on the state diagram need be changed from pure probabilities to statistical distributions (mean and standard deviation).  Readers are invited to make comments about how those distributions might look.

Randomly Right: the Mathematics

iscrete mathematicians will be able to bring all kinds of tools to the calculation: Markov processes and probability theory.  Seven years went by before someone actually did.

Meanwhile, let's just take a simplified look at the problem.  Start with a thought experiment that calls for the tossing of a coin six times and figuring out the probability that six heads will come up in sequence: HHHHHH.  One chance in 64, right?  We can write that probability p(HHHHHH)=1/64.  Same for six tails: p(TTTTTT)=1/64.  The probability that either will occur is the sum, p(HHHHHH)+p(TTTTTT)=1/32.  So, if we carry out 32 independent experiments, tossing a coin six times in each experiment, then we would expect to have maybe one of the experiments come up as a success.  We observe that 32 such experiments requires tossing the coin 6*32=192 times.  Hey, that's less than 200 right there.  Exclamation point withheld, because...

...if that were the basis of Dr. Hill's criterion, then he would be correct only about half the time in accusing his students of faking their tosses.  Hardly what he called "overwhelming odds."  Still, for the sophisticated student, this simple formulation affords a threshold value for successful faking, for we see that in his or her total of n mandated tosses, he or she should assure the presence of strings with length s such that s < n / 2s-1.
Now consider a 6-toss experiment in which almost six heads in sequence appear, THHHHH. The probability for that is one chance in 64, p(THHHHH)=1/64, just like any other combination of six tosses.  Ah, but the first toss in the next independent experiment might be an H.  Of course, H and T are equally likely, such that p(H)=p(T)=1/2.  If H does come up, we have our six heads in sequence, five from one experiment and the sixth from the first toss in the next experiment.  The joint probability for that is p(THHHHH)*p(H)=1/128.  Same for p(HTTTTT)*p(T)=128, so the probability of either is 1/128+1/128=1/64.  In the 32 6-toss experiments conducted within 200 toss, that increases the quality of Dr. Hill's criterion by some amount; however, since the experiments are now overlapping, they are no longer independent, so some of that "quite involved calculation" gets brought into the picture here.

Likewise, for other successive 6-toss experiments...

p(TTHHHH)*p(HH)+ p(HHTTTT)*p(TT)=1/128
p(TTTHHH)*p(HHH)+ p(HHHTTT)*p(TTT)=1/256
p(TTTTHH)*p(HHHH)+ p(HHTTTT)*p(TTTT)=1/512
p(TTTTTH)*p(HHHHH)+ p(HHHHHT)*p(TTTTT)=1/1024
The detection does get improved further, inasmuch as the solution says, "in a series of 200 tosses, either heads or tails will come up six or more times in a row."  Thus, it is not required that all tosses at the beginning of the first pair of 6-toss experiments be the same.  If expressions of the form p(xxxHHH) are allowed, then each such probability is increased.

By now the overlapping of our simple thought experiments will have obliterated any numerical precision.  It would be neat, though, to have a specific number for the probability that in 200 tosses, at least six consecutive heads or six consecutive tails will appear.

ore than seven years after the publication of Randomly Wrong, the following e-mail message was received from Ryan Johnson, a graduate student in the department of Electrical and Computer Engineering at Carnegie Mellon University and obviously a sophisticated puzzle solver:
 

I was reading your site instead of studying for a queuing theory exam, and I realized that this problem can be modeled as a discrete time Markov chain. The trick was to realize that 
(a) for a fair coin it doesn't matter whether a toss comes up heads or tails, only whether it matches the previous one, and 
(b) we don't care how many runs there are (or how long), just so we see at least one run of length >= 6. 
The resulting chain has a transition matrix given by: 
P = [[0    1.0000         0         0         0         0         0]
     [0    0.5000    0.5000         0         0         0         0]
     [0    0.5000         0    0.5000         0         0         0]
     [0    0.5000         0         0    0.5000         0         0]
     [0    0.5000         0         0         0    0.5000         0]
     [0    0.5000         0         0         0         0    0.5000]
     [0         0         0         0         0         0    1.0000]]
Most of its states are transient, but we don't want the limiting probabilities anyway. 

Raising P to the 200th power results in:

P^200 = [[0    0.0176    0.0090    0.0046    0.0023    0.0012    0.9653]
         [0    0.0173    0.0088    0.0045    0.0023    0.0012    0.9659]
         [0    0.0168    0.0085    0.0043    0.0022    0.0011    0.9671]
         [0    0.0156    0.0079    0.0040    0.0021    0.0010    0.9693]
         [0    0.0133    0.0068    0.0034    0.0018    0.0009    0.9738]
         [0    0.0088    0.0045    0.0023    0.0012    0.0006    0.9827]
         [0         0         0         0         0         0    1.0000]]
The top right entry (1,7) is the probability of getting 6+ heads/tails in a row in 200 flips or fewer, assuming a fair coin. We only need to consider P^200 because state 6 is "sticky" and cannot be left, once entered. So, with 96.5% probability a sequence of 200 coin flips will yield 6 or more heads/tails in a row at some point.

Those who crave an exact answer are free to evaluate the following polynomial with p = 0.5. "Quite involved" indeed!

 
p^5*(1
+p
+2*p^2
+4*p^3
+8*p^4
+16*p^5
+31*p^6
+61*p^7
+120*p^8
+236*p^9
+464*p^10
+912*p^11
+1793*p^12
+3525*p^13
+6930*p^14
+13624*p^15
+26784*p^16
+52656*p^17
+103519*p^18
+203513*p^19
+400096*p^20
+786568*p^21
+1546352*p^22
+3040048*p^23
+5976577*p^24
+11749641*p^25
+23099186*p^26
+45411804*p^27
+89277256*p^28
+175514464*p^29
+345052351*p^30
+678355061*p^31
+1333610936*p^32
+2621810068*p^33
+5154342880*p^34
+10133171296*p^35
+19921290241*p^36
+39164225421*p^37
+76994839906*p^38
+151367869744*p^39
+297581396608*p^40
+585029621920*p^41
+1150137953599*p^42
+2261111681777*p^43
+4445228523648*p^44
+8739089177552*p^45
+17180596958496*p^46
+33776164295072*p^47
+66402190636545*p^48
+130543269591313*p^49
+256641310658978*p^50
+504543532140404*p^51
+991906467322312*p^52
+1950036770349552*p^53
+3833671350062559*p^54
+7536799430533805*p^55
+14816957550408632*p^56
+29129371568676860*p^57
+57266836670031408*p^58
+112583636569713264*p^59
+221333601789363969*p^60
+435130404148194133*p^61
+855443850745979634*p^62
+1681758329923282408*p^63
+3306249823176533408*p^64
+6499916009783353552*p^65
+12778498417777343135*p^66
+25121866431406492137*p^67
+49388289012067004640*p^68
+97094819694210726872*p^69
+190883389565244920336*p^70
+375266863120706487120*p^71
+737755227823635631105*p^72
+1450388589215864770073*p^73
+2851388889419662535506*p^74
+5605682959145114344140*p^75
+11020482528724983767944*p^76
+21665698194329261048768*p^77
+42593641160834886466431*p^78
+83736893732453908162789*p^79
+164622398575488153790072*p^80
+323639114191831193236004*p^81
+636257745854937402704064*p^82
+1250849793515545544359360*p^83
+2459105945870256202252289*p^84
+4834474998008058496341789*p^85
+9504327597440628838893506*p^86
+18685016080689426484551008*p^87
+36733774415523915566397952*p^88
+72216699037532285588436544*p^89
+141974292129194314974620799*p^90
+279114109260380571452899809*p^91
+548723890923320514066906112*p^92
+1078762765765951601649261216*p^93
+2120791757116379287732124480*p^94
+4169366815195226289875812416*p^95
+8196759338261258264777004033*p^96
+16114404567262135958101108257*p^97
+31680085243600951402135310402*p^98
+62281407721435951202621359588*p^99
+122442023685755523117510594696*p^100
+240714680556315819945145376976*p^101
+473232601774370381625513749919*p^102
+930350798981478627292926391581*p^103
+1829021512719356303183717472760*p^104
+3595761617717276655164813585932*p^105
+7069081211748797787212116577168*p^106
+13897447742941279754479087777360*p^107
+27321662884108189127332661804801*p^108
+53712974969234899627372397218021*p^109
+105596928425750442951561076963282*p^110
+207598095233783609247957340340632*p^111
+408127109255818420708702564104096*p^112
+802356770768695561662926040430832*p^113
+1577391878653282934198519419056863*p^114
+3101070782337330968769666440895705*p^115
+6096544636248911494587771804828128*p^116
+11985491177264039379927586269315624*p^117
+23562855245272260339146469974527152*p^118
+46323353719775825116630013908623472*p^119
+91069315560898367299061508398190081*p^120
+179037560339459403629353350355484457*p^121
+351978576042669895764118928906140786*p^122
+691971660908075752148310271542965948*p^123
+1360380466570879243957474073111404744*p^124
+2674437579421982662798318132314186016*p^125
+5257805843283066958297574756230181951*p^126
+10336574126226674512965796162104879445*p^127
+20321169676410679130167473395303618104*p^128
+39950367691913282508186636519064270260*p^129
+78540354917255685772415798965017135776*p^130
+154406272255089388882033279797720085536*p^131
+303554738666895710805768984839209989121*p^132
+596772903207564747098572173516315098797*p^133
+1173224636738718815066976873637326579490*p^134
+2306498905785524347625767110755588888720*p^135
+4534457456653793009479118422546160641664*p^136
+8914508641052496630076203565294601197792*p^137
+17525462543438097549346638145749992406463*p^138
+34454152183668630351594704117983669714129*p^139
+67735079730598541888122431362330012848768*p^140
+133163660555411559428619095613904436808816*p^141
+261792863654169325847759072805262712975968*p^142
+514671218667286155065441942045230824754144*p^143
+1011816974791134212581537245944711657101825*p^144
+1989179797398599794811479787771439644489521*p^145
+3910624515066601047734837144180549276130274*p^146
+7688085369577790536041055192747194115451732*p^147
+15114377875501411746234351312689125517927496*p^148
+29714084532335537337403260683333020211100848*p^149
+58416352089879940462224984120721328765099871*p^150
+114843524382361281129638488453671217885710221*p^151
+225776424249655961211542139763161886495290168*p^152
+443864763129734131887043224333576578875128604*p^153
+872615148383966852027852097354464032232329712*p^154
+1715516212235598166718300934025595044253558576*p^155
+3372616072381316392974376883930468759742017281*p^156
+6630388620380271504819115279407266301598324341*p^157
+13035000816510887048426688419051370716701358514*p^158
+25626136869892039964966333613769164854527588424*p^159
+50379658591400113077904815130183865676822847136*p^160
+99043800970564627989091329326342136309392135696*p^161
+194714985868747939585208281768753803859042254111*p^162
+382799583117115607665597448258100341416486183881*p^163
+752564165417720328282768208097149312116271009248*p^164
+1479502193965548616600570082580529459378014430072*p^165
+2908624729339697120123235350030875053079206013008*p^166
+5718205657708829612257379370735407969849019890320*p^167
+11241696329548911284929550459702062135838997526529*p^168
+22100593075980706962193503471146023930261508869177*p^169
+43448621986543693596104238734194898548406746729106*p^170
+85417741779121838575607907385809267637435479028140*p^171
+167926858828903980031092579421587660221791752043272*p^172
+330135512000099130449927779472439912473734484196224*p^173
+649029327670649349614926008485177762811629970865919*p^174
+1275958062265317992267658513499209501692998432862661*p^175
+2508467502544092290939212788264224104837590118996216*p^176
+4931517263309062743302817669142638942037744758964292*p^177
+9695107667789221506574542758863690223853697765885312*p^178
+19060079823578343882699157738254940535233661047574400*p^179
+37471130319486038415783389468024703307655692124282881*p^180
+73666302576706758839299120422550197113618385815703101*p^181
+144824137650869425387659028056836170122399181512409986*p^182
+284716758038429788032015238444529701302760618265855680*p^183
+559738408409070354557455934130195712381667538765826048*p^184
+1100416736994562365232212710522136484228101416484077696*p^185
+2163362343669638692048642031576248265148547140843872511*p^186
+4253058384762570625257984942729946333183475895872041921*p^187
+8361292631874271825128310857403056496244552610231673856*p^188
+16437868505710113862224606476361583291186344602197492032*p^189
+32315998603011157369891757018592970869991021665629158016*p^190
+63531580469027752374551301326663805255753941914774238336*p^191
+124899798594385866057053960621751362246359336688704604161*p^192
+245546538804009161488849936300772778159535197481537166401*p^193
+482731784976144051152571561744142499822825842352842658946*p^194)

Applying the criteria set forth in Discovering Assumptions, this solution would have warranted a grade of 'C'.  Ryan Johnson was not satisfied with that.  "To earn a grade of 'B'," he wrote, "I should point out that this approach will work for any (k, N) where this case is (6, 200).  For the 'A', we could ask, 'in a series of 200 tosses, what is the probability that the longest run of either heads or tails is six?'  I'm not sure right off how to solve it, but it would probably involve a second chain that goes out to 7 before 'sticking'.  Simply subtracting the probability of 'sticking' at 7 in the second chain from the answer to the first chain might do it."

Randomly Right: The Model

mpiricists may enjoy demonstrating the phenomenon with a simple spreadsheet. The sophisticated solver knows how to use a spreadsheet to create an interactive 'model' of a problem.

Spreadsheet conventions used here include...

For the formulas below, you will need six columns (A...E) and 201 rows.

For n = 1...200, let...

To carry out experiments, simply make entries anywhere outside the table, which operates the random number generators, simulating 200 tosses simultaneously. Each such experiment simulates the efforts of one student tossing coins as his or her assignment.

Watch the two locations D201 and E201. One or both of them will show non-zero values for nearly every honestly random experiment.
 
 


Home Page
Puzzle Page
Math and Models
The Puzzle as a Literary Genre