|
Copyright ©2016 by Paul Niquette. All rights reserved. |
|||||
"Necessity is the mother of invention" must be the most popular aphorism relevant to technology. However, often as not, the opposite is true, as shown in Mother of Necessity. Here is a proposal for a case in that point. The sketch above depicts the answer to a question arising from the idle curiosity of a retired systems engineer. What
is the maximum eccentricity
of a 24-hour geosynchronous orbit?
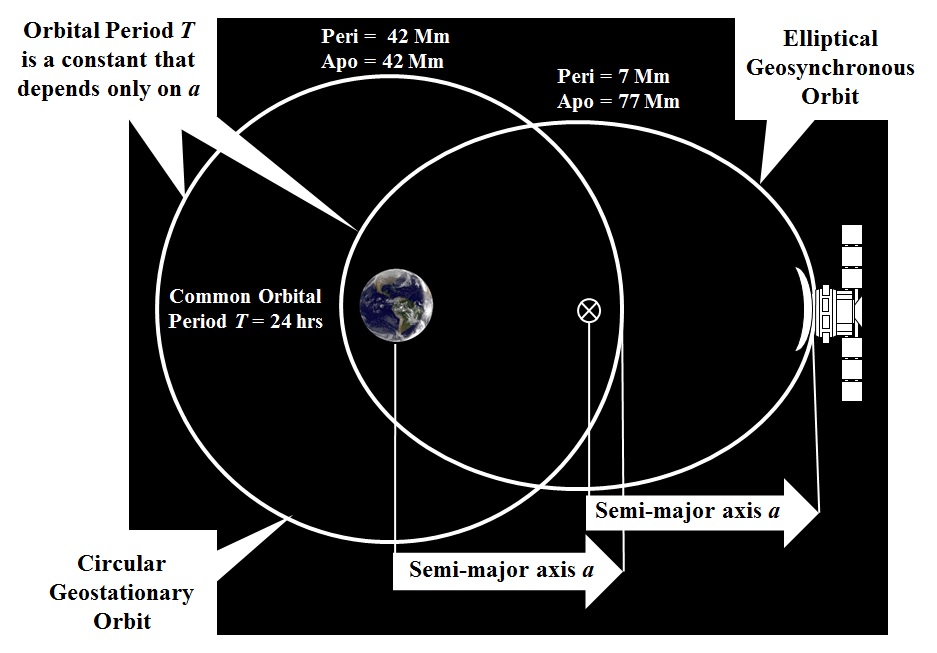
The familiar geostationary orbit (commonly named GEO) is circular and is populated by more than three hundred satellites. The orbital period T = 24 hours, which matches the rotation of the earth. Operating in the equatorial plane, each GEO satellite will appear stationary in the sky from wherever on earth it can be seen. That gives GEO its most valuable feature... Ground-based directional antennas, including roof-top 'dishes', can be fixed in both azimuth and elevation. Thus, we see in the sketch that GEO's perigee and apogee are both 42 Mm (26,250 miles), which is 36 Mm (22,250 miles) in elevation MSL.Also depicted in the sketch is the elliptical geosynchronous orbit (eGEO will be our name for it). The eGEO is an invention -- hey, an invention without a mother. The orbital period of the eGEO equals that of the GEO T = 24 hours, which also matches the rotation of the earth; however... A satellite operating in an eGEO will not be stationary in the sky. It will be synchronous with the rotation of the earth, such that at any given point in its orbital plane, an eGEO satellite will pass directly overhead at the same time every day. Twice, actually.As legended in the sketch, orbital period T depends only the semi-major axis a and, of course, vice-versa: a depends only on T. Sophisticated solvers may enjoy showing that by keeping a = 42 Mm (26,250 miles), one can derive the parameters for the eGEO with an apogee of 77 Mm (48,125 miles) and perigee of 7 Mm (4,375 miles). The proposed eGEO is deliberately limited by its perigee to 7 Mm (4,375 miles), which is 600 Km (375 miles) in elevation to keep the eGEO clear of Hubble and the International Space Station. Accordingly, here is the answer to our question... What
would be an
application
for a
satellite in
an eGEO?
 To
answer that question, solvers will find two points in
the eGEO most interesting: apogee at 77 Mm (48,125
miles) and perigee at 7 Mm (4,375 miles), measured
from the center of the earth, with its radius of 6.4
Mm (4,000 miles). Suppose a satellite S in an equatorial eGEO reaches apogee over some point P on the earth’s surface (nadir) at, say, midnight. At midnight the next day, S will again reach apogee over P. Indeed, every day. Halfway in between, S will pass through its perigee. Meanwhile, the earth will have rotated halfway ‘round. Thus at high noon, S will be at perigee over P.
Simple: 360 degrees in 24 hours (15 deg/hr) – same as the earth itself. Duh.The renowned astronomer might suggest that for an elementary solution we give our attention to…
Nota bene: At apogee and perigee, a satellite in an eGEO will comply with those angular velocities relative to earth (8.2 deg/hr and 90 deg/hr) in any orbital plane from equatorial to polar. Hmm.
 |
|||||
| eccentricity
= (apogee - perigee) / (apogee + perigee) = (77 - 7) / (77 +7) = 0.833 |
|||||
