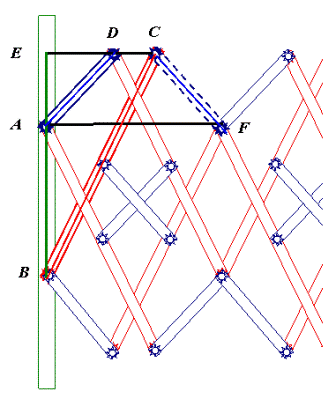Support Separation AB,
Long Link BC, and
Short Link AD = CF

As the Linear Linkage expands, the following trigonometric relationships will always apply:

BE = BC cos ABC + AD cos DAE

...and since AD = CF...

BE = BC cos ABC + CF cos DAE

...which keeps the point F at the same elevation as A for all positions of the linkage and solves the Linear Linkage puzzle...

ome solvers may be astonished to learn that the link-lengths do not matter -- that any number of Linear Linkages can be designed with no sliding elements.  Of course, there will be application-specific dimensions to consider for, say, optimizing the span ratio. 

One thought is that the Linear Linkage might play a role in deploying solar panels in space, as suggested by this photograph.  You are invited to send your ideas here. 

International Space Station's solar array panels are featured in this image 
photographed by the Expedition 17 crew in August 2008. Credit: NASA