Copyright ©2011 by Paul Niquette All rights reserved. |
|
 e
need first to make a reasonable assumption
about the meaning of a 'perfect ice cube' in the puzzle formulaton: "Given a
perfect ice cube, what is the height of its tip above
the surface of the water on which it is floating?"
Let us take the expression to mean that all three of the
cube's dimensions are equal to each other and equal to
some value, which might be an inch, say, or 2.54 cm or
whatever. Using the dimensionless term 'unity'
with symbol 1 as
its value, the perfect cube's volume is given as 1 x1 x 1 = 13 = 1.
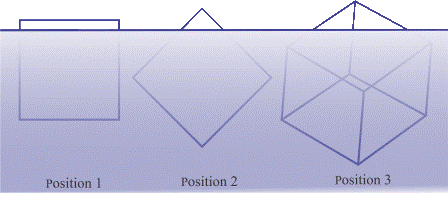
Solvers are invited to assign h to represent the unknown 'height' in the phrase "height of its tip," which can be expressed as a fraction of 'unity'. Now, a cube, perfect or not, has a total of eight 'tips' (all right, corners). Depicted in the sketch are three orientations of the 'perfect ice cube' floating in water. In Position 1, the ice cube has four tips above the water-line; in Position 2, two; in Position 3, only one Tip of the Ice Cube is visible. Whatever the orientation, according to the graph given in the puzzle, about 1/10th of the ice cube's mass and therefore 1/10th of its volume must be above the water line.
Position 1: The part of the cube above the waterline is a rectangular parallelopiped. Its cross-sectional area will be given by h x 1, and its volume will be given by h x1x1. We can calculate the unknown h = (1 x1 x 1)/10 = 0.10. Position 2: The part of the cube above the waterline is a right-triangular prism. Its cross-sectional area is given by h2, and the volume above the waterline is given by h2 x1. We can calculate the unknown h = [(1 x1 x 1)/10]1/2 = 0.32. Position 3: The part of the cube above the waterline is a three-sided pyramid. Its volume will be given by b h/3, where b is the area of its base at the waterline...
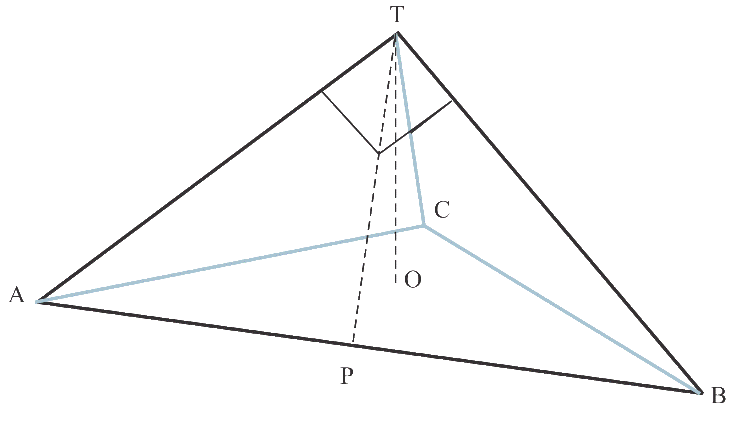
For convenience, let x = AB, such that
PT = x/2.
It
is easy to see that APT forms an isosceles right
triangle with AT as its hypotenuse. We find that
x = 21/2 AT by
the Pythagorean
Theorem and some algebra. This expression gives each edge of the base b which will be used to calculate the volume of the pyramid. Thus b = x2 31/2 / 4 and b h/3 = h3 / 3 = (1 x1 x 1)/10. We can solve for h = 0.67. Accordingly, our solutions (plural) for the puzzle can be summarized as follows: The height of the tip of a perfect ice cube above the surface of the water on which it is floating...
Consider the ice cube orientations modeled above. Position 1 had the lowest tip-height (10%) and essentially zero approach distance. Position 2 had a range of tip-heights (up to 32%) and variable distances depending on the approach direction. Position 3 had the highest tip-height (67%) and the largest approach distance, making it probably the safest in a maritime setting; however...Sophisticated solvers will note that in Position 3, the ice cube would not be stable, inasmuch as perturbations will allow the center of buoyancy to become mis-aligned with the center of mass, capsizing the ice cube toward Position 2 and eventually to Position 1, which is stable. By the way, any natural iceberg must have an elongated dimension, which will pitch it over into a horizontal orientation. Accordingly, solvers of the Tip of the Ice Cube puzzle will be skeptical of phantasmagorical claims such as were made for the iceberg in this photograph. |
ketched below
is the base b of
the pyramid as an equilateral triangle ABC, with point
T representing the 'tip' projected vertically to point
O, making the unknown h =
TO. One of the sloping surfaces of the pyramid
ATB is viewed from a vantage point that emphasizes the
cube's right angle at T. Point P has been place
halfway between A and B and connected to T by a
construction line bisecting the right angle and making
PT = AP = BP = AB/2. 
ack on that
dark night in April 1912, some dozen years before the
first 