Here Comes the Sun -- Solution

Here Comes the Sun

From the preflight information provided in the puzzle, we learn the following:

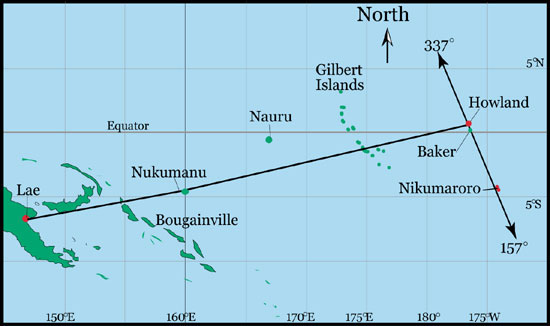
{1} Date of Flight ~~~~~~~~~~~~~~~~~~~~~~~~~~~ July 2, 1937
{2} Take-off Time at Lae ~~~~~~~~~~~~~~~~~~~~~~~ 0000 GCT
{3} Estimated Time Enroute (ETE) Lae to Howland ~~~~ 18 hours
{4} Estimated Time of Arrival (ETA) at Howland ~~~~~ 1800 GCT

From the map below, we are able to confirm geographical locations as follows:

TIGHAR Earhart Project used by permission

{5} Lae ~~~~~~~~~ 6.733 S 147.000 E
{6} Bougainville ~~~~ 5.098 S 154.891 E
{7} Nukumanu ~~~~~~ 4.333 S 159.700 E
{8} Gilbert ~~~~~~~~~~ 0.975 S 174.789 E
{9} Howland ~~~~~~~~~~ 0.803 N 176.634 W

The Sunrise and Sunset Calculator offers four different kinds of each, sunrise and sunset. Sophisticated solvers will study the relevant definitions and conclude that, for navigational purposes, the demarcation between day and night of greatest concern to Fred Noonan would have been "Nautical" not "Official."

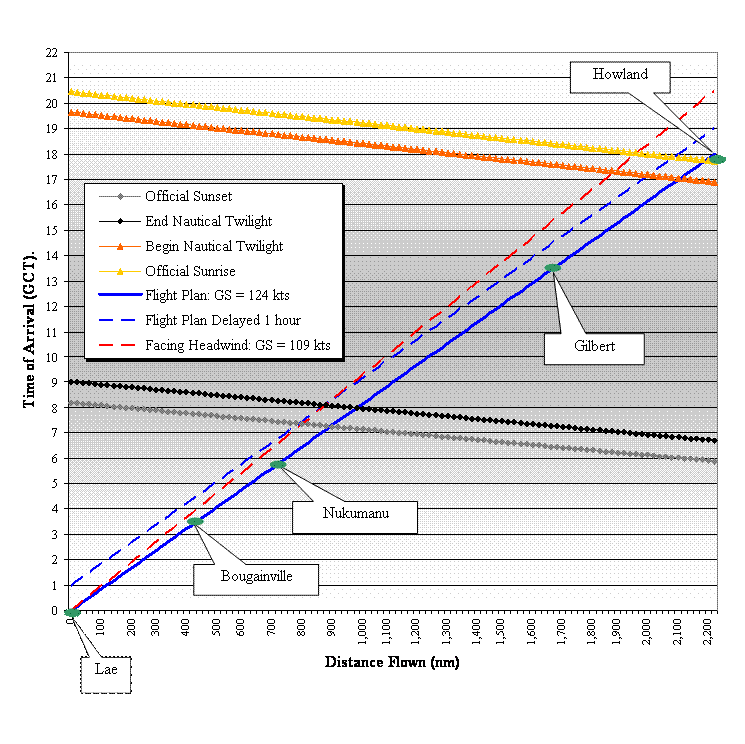
Consider first...

{10} "Official Sunset" at Lae ~~~~~~~~~~~~~~~~~~~08:08 GCT

...leaves more than three quarters of an hour of twilight during which star-sightingss would be doubtful for celestial navigation. This condition would prevail until...

{11} "Nautical Sunset" at Lae (end of twilight) ~~~~~~ 08:57 GCT

Thus, nearly nine hours of daylight at Lae remained after take-off at 0000 GCT, during which navigation by dead reckoning would be allowed based on visual identification of landmarks, including, presumably one of the islands in the Bougainville chain. Using the calculator again we find...

{12} "Nautical Sunset" at Bougainville ~~~~~~~~~~~~ 08:28 GCT

...raising the question, Will the flight reach Bougainville before the sky goes dark there? -- in aviation parlance: "What is the ETA for Bougainville?" To answer questions like that, solvers must be able to figure out leg-distances and time-intervals. Here is one method for such estimations, starting with two reminders...

Anywhere on earth, one minute of latitude is one nautical mile (60 nm per degree).
Near the Equator, one degree of longitude is likewise equal to 60 nm.

Between Lae and Howland, the flight will make changes in latitude and longitude of 7.535^o and 36.366^o, respectively. Given those two geographcial coordinates Fred Noonan would have applied spherical trigonometry to calculate the great circle distance from Lae to Howland. Purists will object, of course, but for this puzzle, solvers can simply use the Pythagorean Theorem for a reasonable estimate of the angular distance as 37.14^o and compute an overall distance of 2,220 nm or 2,556 statute miles (sm) for the historic leg. From {3} we see that Noonan estimated a flying time of 18 hours, allowing us to estimate a ground speed of 123.8 knots (142.5 mph).

The distance from Lae to Bougainville as about 484 nm (557 sm) for an ETE and ETA of 3:55 GCT. According to {12}, that means about 4:23 of daylight to spare.

Using the same method, we find that proceeding toward the east at 123.8 knots, the ETA for Nukumanu, 294 nm (339 sm) farther along from Bougainville, will be 6:17 GCT, where...

{13} "Nautical Sunset" at Nukumanu ~~~~~~~~~~~ 08:10 GCT

...affords almost two hours of daylight to spare for visual dead reckoning to that checkpoint. A visual confirmation of the flight's position overhead Nukumanu following dead reckoning for 2:22 with no ground references available, might have become crucial, inasmuch as Noonan planned to make a slight change in course there.

Solvers are urged to take notice that while Earhart and Noonan were making their way eastward at 123.8 knots, "Nautical Sunset" is moving westward 360^o every 24 hours, thus at 900 knots (1,036 mph).

Upon arrival overhead one of the Gilbert islands at 13:45 GCT, the flight would find the islands in total darkness, inasmuch as...

{14} "Nautical Sunset" at Gilbert ~~~~~~~~~~~~~~ 07:18 GCT

...means that Noonan would have been depending on celestial navigation, taking star fixes, for some amount of time (see the graph below). Meanwhile...

{15} "Nautical Sunrise" at Gilbert ~~~~~~~~~~~~~17:34 GCT

...results in morning twilight that will end the darkness at Gilbert some time after the Electra has passed overhead (again, see the graph below). Of course, Noonan's main concern would have been...

{16} "Nautical Sunrise" at Howland ~~~~~~~~~~~16:57 GCT

...which precedes the planned ETA of 18:00 GCT by just over an hour. Morning twilight and sunrise would assure plenty of time "for a landing on an unlighted runway" as mentioned in the puzzle. Given...

{17} "Official Sunrise" at Howland ~~~~~~~~~~~~17:46 GCT

...the sun will have been above the horizon for 14 minutes before the ETA at Howland. Indeed, the sun would be 3.5^o above the horizon as the Electra touched down.

Accordingly, using just the pre-flight planning information for solving the Here Comes the Sun question, "Did Fred Noonan choose the appropriate take-off time?" our answer is...

Yes, but...

Suppose departure of the flight were delayed by, say, an hour at Lae. It is easy to see that for Fred Noonan, this would not present a navigational problem either at Bougainville or Nukumanu. There would still be plenty of daylight for dead reckoning, including a most welcome half-hour to spare at Nukumanu for making the course change. Likewise, the delayed arrival at Howland would afford Amelia Earhart an extra hour in sunlight to complete the approach and landing. Headwind during the flight would have a similar effect, delaying arrivals at every checkpoint, such that the ATA at Howland would suffer the longest delay.

So, then, why that little "but" in the solution to the Here Comes the Sun puzzle?

Delaying the arrival time at Howland also advances the transition from celestial navigation in the dark to dead reckoning in daylight, inasmuch as "Nautical Sunrise" would be relentlessly rushing westward toward the Electra at a relative ground speed of 1,180 mph (900 + 123.8 knots).

Uh, oh.

Noonan's last star-fixes must be completed farther away from Howland because of the headwind. Sophisticated solvers will surely enjoy determining exactly how much farther away -- and perhaps also generalizing the analysis to address any amount of flight delay.

The graph below is a bit unusual, in that it shows time-related events as dependent variables plotted against fixed locations along the planned flight path.

Here are five observations...

All the sun events can be seen to make the 2,220 nm trip from Howland to westward to Lae in about two and a half hours, while the planned Earhart-Noonan flight would require 18 hours to make good the same distance in the opposite direction.
The twilight transition from visual dead reckoning to celestial navigation is seen to take place at about 0800 GCT, 880 nm from Lae, well beyond Nukumanu.
As mentioned in {14} and {15}, the planned over-flight of Gilbert would take place after about five and a half hours of darkness, with about three and a half more to go.
The transition from celestial navigation at night back to visual dead reckoning is seen to take place at about 1700 GCT 150 nm from Howland.
If the flight were to face a headwind greater than planned by, say, 15 knots (see the red-dashed line), arrival at Howland would be delayed as much as two and a half hours, which is a subject for another puzzle (Live Reckoning).

Most relevant to our Here Comes the Sun solution is the solemn reality that with Fred Noonan's Last Celestial Fix logged before 1715 GCT, the Electra will be 330 nm from Howland, thence forced to dead reckon over a featureless ocean until... well, until radio direction finding becomes established with Howland for homing. Exclamation point, anyone?