f_(n+1) = f_n + f_(n-1)

f_n = 86,267,571,272

You can start over at 0, 1, 1, 2, 3, ..., 86,267,571,272, but that will take quite awhile. You may be pleased to know there's another way.

n the mid-eighteenth century, Robert Simson at the University of Glasgow discovered that the ratio of two successive Fibonacci numbers 'tends' toward a constant. Figuring this out might have kept an old-time mathematician off the streets for weeks. For the sophisticated solver, the derivation is elementary.

With a modern calculator, one can effortlessly reconfirm Simson's discovery in seconds.

Care to try? Take any Fibonacci number and divide it by the next number in the series. Use 21 and 34, for example. You get 0.61764705. Or take the next pair, 34 and 55, which produces the ratio 0.618181818...

By the 29th and 30th number, you will see that the ratio has settled down -- 'converged,' in math-talk -- so that one can perceive no change in its value even with many digits of precision. The ratio approaches the constant value of...

Congratulations, you have found the value of something called  (phi, usually pronounce FAE), which is a Greek letter, like 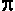 (pi, usually pronounced PAE), commonly used to denote the ratio of a circle's circumference to its diameter, and 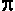's value, 3.14159..., thanks to computers, has grown in precision to over 10 million decimal places. Likewise,  also represents a ratio and is often called the "Golden Mean" or, in geometric form, "Golden Section."

=  f_n / f_(n+1), so then...
f_(n+1)  =  f_n / , and for the puzzle at hand...
f_(n+1) =  86,267,571,272 / 0.61803398874989484820...

139,583,862,445

Derivation of Simson's Discovery

The (n + 1)st Fibonacci number is derived from the previous two as follows:

f_(n+1) = f_n + f_(n-1)

  f_(n-1)  /  f_n  =  f_(n+1) /  f_n  - 1

Now, for Robert Simson's assertion to hold, as n approaches infinity (What an oxymoron! -- "approaching" that which cannot be approached?), the ratio of each Fibonacci number to its successor is a constant. Thus,...

 f_(n-1) / f_n approaches f_n / f_(n+1)

Let's make it easy on ourselves by setting both ratios equal toand rewriting...

=  1/  - 1.

²+ - 1 = 0

= (5^1/2 - 1) / 2 = 0.618033988750.

y the way, mathematicians have classified  along with 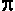 as an "irrational number," which seems like an irrational choice of words, for the case at hand, inasmuch as irrational numbers -- by definition -- cannot result from the ratio of whole integers, which is exactly what each Fibonacci number happens to be.

The key to this paradox hides within that infinity business in the derivation provided above.

 

Where parallel lines meet, so too do the rational and the irrational. -- Paul Niquette, 1997

{Return}

Fibonacci Fantasy in a Spreadsheet

The sophisticated solver knows how to use a spreadsheet to create an interactive 'model' of a problem.

Spreadsheet conventions used here include...

• columns designated by letters A, B,...
• rows designated by numbers 1, 2...
• fixed references are denoted by $
• arithmetic operators +, -, *, /, sqrt(radicand)

A1 = 0 ~~ first number of the series f₁
A2 = 1 ~~ second number of the series f₂
A3 = A1 + A2 ~~ the Fibonacci Recursion Formula
A4 = A2 + A2 ~~ pasted entries with relative references
...
An = A(n-2) + A(n-1) ~~ for any size of table (let n = 50, say).

To test Simson's Ratio, set...

B2 = A3 / A2 ~~ ratio of  f₂ / f₃
B3 = A4 / A3 ~~ pasted entries with relative references
...
Bn = A(n+1) / An ~~ ratio f_n / f_(n+1)

You will see that B19 = 0.618033963, which is a good approximation of . How good? Well you might place the formula forin the table (at C1 say)...

= (5^1/2 - 1) / 2
C1 = (SQRT(5) - 1) / 2

Cn = (C$1 - Bn) / C$1

Now, what happens if we change the beginning numbers in A1 and A2?

Watch the entries grow: 11, 18, 29, 47,... Take out your calculator and figure those ratios of succeeding values -- or scan your spreadsheet. They tend to the same value, 0.618033988750! That Golden Section turns up again.

Experimentation with any number of seed numbers always shows that outcome. Consider, too, the series started by 100 and 2. Notice how fast the numbers grow. The 34th exceeds the population of the U.S.; the 40th, the population of the world. Yet, those ratios steadfastly approach the same value .

You can plant a negative seed like -123 alongside, say, 77. After some vacillation, plus and minus, the numbers come out positive and sail off to infinity -- at Simson's fixed ratio still. Another amazement: By changing the 77 to 76, the consequent Fibonacci numbers stumble into a black hole of unlimited negativity -- but the ratio  still holds. No exclamation point, please.