|
Copyright ©2011 by Paul Niquette. All rights reserved. |
|
  What
sets the limit for the speed of a train? Curves,
mostly. Climbing
a grade, of course, speed will depend to some extent on
horsepower-to-weight
ratio. Coming down, it's curves again. On level
track, wind resistance
will play a role, as explored in the World's Fastest
Train puzzle. Tracks are seldom perfectly
straight for great
distances. There are hills and cities to steer
around and stations
to line up with. What
sets the limit for the speed of a train? Curves,
mostly. Climbing
a grade, of course, speed will depend to some extent on
horsepower-to-weight
ratio. Coming down, it's curves again. On level
track, wind resistance
will play a role, as explored in the World's Fastest
Train puzzle. Tracks are seldom perfectly
straight for great
distances. There are hills and cities to steer
around and stations
to line up with.
On the right we see a train negotiating a curve to the left. Superimposed are the unbalanced forces that tend to tip the train toward the outside of the curve, much as in the Circling: Ground and Sky puzzle.
Sharp curves are out of the question. For speed, radius of curvature R needs to be made as long as possible, but there are often limitations imposed by terrain or land-use commitments.
Figure 2 shows how superelevation, symbolized by E, can be used much like a banked highway to balance the rail forces (Fi = Fo ) thereby allowing trains to operate faster than might otherwise be possible along curvatures in the trackway. For given values of R and E, the two track forces can be balanced at only one particular train train speed, VBALANCED... Fc / W = E / G, and......where g = the acceleration of gravity (32.2 ft/sec/sec).
Every segment of trackway must be certified with what is called a 'civil limit', which specifies the maximum speed that a train can operate on it. In additon to the dimensions of curves as indicated here, civil limits must take into consideration all trackway conditions, including grades, switches, and station platforms.
Of course, trackways are never designed to change abruptly from straight to curved and back again. Instead, the rails are given a 'spiral' shape, gradually changing radius of curvature, between infinitely long, for straight trackway, to a fixed radius R, for a circular segment in the 'alignment'. Along the spiral, superelevation changes linearly from zero to its value E as indicated in Figure 4.
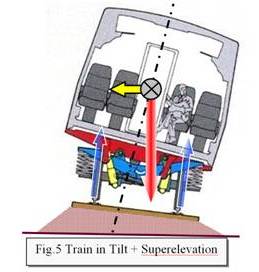
The tilting train was invented to overcome discomfort for passengers, the first being put into service in 1938. Figure 5 is a sketch of a high-speed passenger car traveling in a curve and tilted by a mechanical device atop the bogie. The tilt angle has been adjusted on the fly so that the passenger apparently experiences no lateral forces. Complete balance might seem to be ideal. It is not.
Figure 6 shows the preferred application. An accelerometer fitted in the first bogie of the train measures lateral forces as the train enters a curve. The signal is processed by computer and sent down the trainline. Computer-controlled hydraulic rams tilt each coach into the curve, up to a maximum inclination of 6.5º. The tilting system compensates for no more than 75% of the lateral force of a curve and is only employed at speeds above 44 mph. Incidents of tilt-train 'sea-sickness' are rare, as 25% of lateral forces are still felt by the passengers.
Cruise Speed ~~~~~~~~~~~~~~~~ VCRUISE = 200 mph
|
|
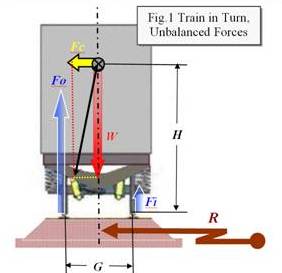 Figure
1 is a sketch of a train-car traveling along a curve
of radius R
on a track with
Figure
1 is a sketch of a train-car traveling along a curve
of radius R
on a track with 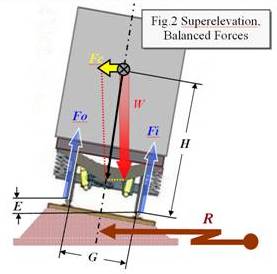
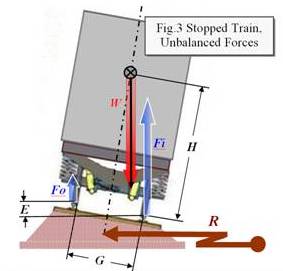 Figure
3 is included here to address another limit, this time
on the values of
superelevation E in view of gravity's
tendency to tip a stopped
train toward the inside of the curve. The effect
is worsened by the
draw-forces between vehicles as the train starts
up.
Figure
3 is included here to address another limit, this time
on the values of
superelevation E in view of gravity's
tendency to tip a stopped
train toward the inside of the curve. The effect
is worsened by the
draw-forces between vehicles as the train starts
up.
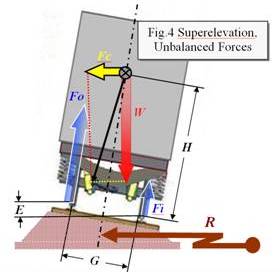 Superelevations
are generally specified for an intentional 'unbalance'
of forces as shown
in Figure 4. Thus, at speeds approaching civil
limits, the train
will tend to be tilted outward from the center of
curvature.
Superelevations
are generally specified for an intentional 'unbalance'
of forces as shown
in Figure 4. Thus, at speeds approaching civil
limits, the train
will tend to be tilted outward from the center of
curvature.
 Meanwhile,
objects inside the train -- in particular passengers
-- will be acted upon
by invisible, gradually changing forces from the left
or the right every
time the train enters a curve from straight, tangent
track.
Meanwhile,
objects inside the train -- in particular passengers
-- will be acted upon
by invisible, gradually changing forces from the left
or the right every
time the train enters a curve from straight, tangent
track.
 According
to an article published by the
According
to an article published by the 