hey
come from all over cyberspace... hey
come from all over cyberspace...
-
collections of funny headlines and bumper stickers;
-
ten-item lists of satirical observations about topical events;
-
reasons why God never got a PhD;
-
how you can tell if you are a geek or a nerd, a redneck or
a liberal.
Often these messages have been relayed over the network so
many times that half your screen gets filled with rows of >>>> angle-brackets.
You receive them from friends and family, associates and e-mail correspondents
-- all eager to share a chuckle or inflict a chortle, to make a point or
simply to satisfy an impulse to communicate.
It's an exponential phenomenon: Every modem on earth
will receive at least x copies of each message after m
forwardings to the nth power. That doesn't happen, presumably,
because some sizable fraction f of the recipients have not
yet become habituated by their respective icons for re-transmissions (the
mathematical expression for which is left as an exercise for the reader).
Most of these gratuitous treasures are anonymous. Permit
me to excerpt from one such message...
|
How Mil Specs Live Forever
The US Standard railroad gauge (distance between the rails)
is 4 feet, 8.5 inches. That's an exceedingly odd number. Why was that gauge
used? Because that's the way they built them in England, and the US railroads
were built by English expatriates...
|
The piece continued with a step-by-step progression of
'why' questions that track (ugh) backwards through history, including...
-
the wheel spacing for pre-railroad tramways,
-
the jigs for building wagons,
-
the separation between old wheel ruts,
-
the roads built by Imperial Rome, and
-
the Roman war chariots.
The answer to the original question, accordingly, is that
the standard railroad gauge of 4 feet, 8.5 inches derives from the military
specifications for an Imperial Roman army war chariot.
In keeping with the cynicism of our times, the piece concludes... |
|
...so, the next time you are handed a specification and wonder
what horse's came up with it, you may be exactly
right. Because the Imperial Roman chariots were made to be just wide enough
to accommodate the back-ends of two war horses.
|
{Optional Anecdote}
With scarcely a moment's thought, I
clicked "Send," after first scarfing up a few nicknames from my address
book and pasting them in the "TO" field. One of them was for Tom Bray,
renown sculptor and didgeradoo prodigy. That was a mistake. Tom's immediate
reply plunged an elderly compulsive into frantic private researches...
"Okay, Mr. Smartypants, what is the
ideal track gauge?"
-
Did the wheel separation on the
-
6th Century BC Etruscan Chariot
-
determine the track gauge for the
-
21st Century AD Railway Truck?
|
-
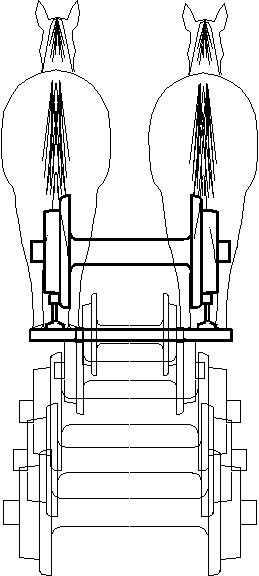
-
Apparently not.
|
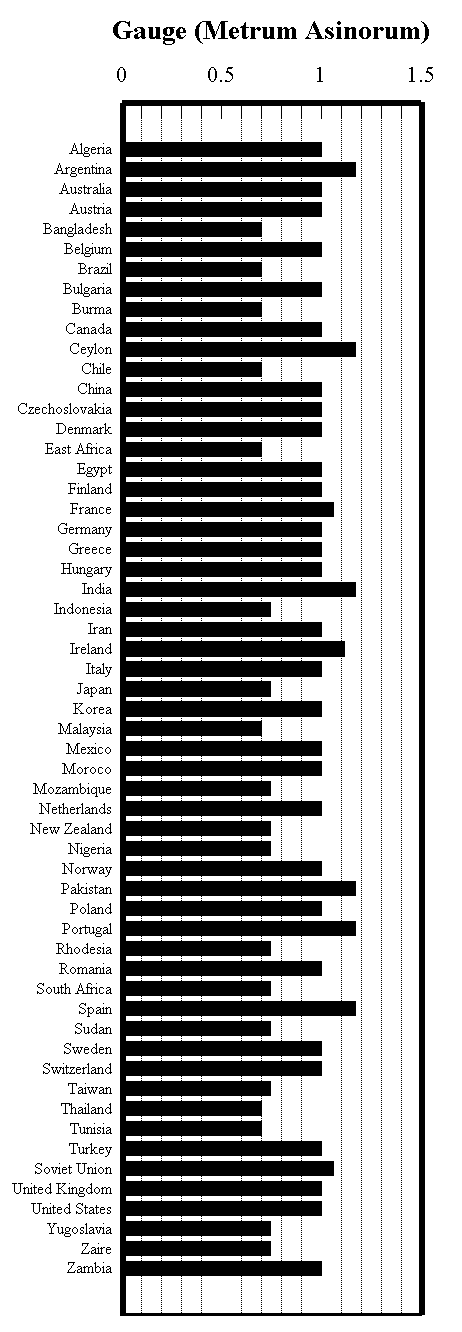
Track
Gauges for Railways of the World
-
This tabulation affords to sophisticated readers a decided advantage for
competing in a game of some unimaginably advanced edition of Trivial
Pursuit.
-
Format: country | year | ownership | gauge | length in miles
-
Algeria | 1862 | 4 ft 81/2 in | 3,071
-
Argentina | 1857 | state | 5 ft 6 in. | 15,462 | metre | 10,715 4 ft 81/2
in | 2,210
-
Australia | 1854 | state | 4 ft 81/2 | 8,302 | 5 ft 3 in.
-
Austria | 4 ft 81/2 | 6,998
-
Bangladesh | 1861 | state | metre | 2,517
-
Belgium | 1835 | state | 4 ft 81/2 | 7,754
-
Brazil | 1854 | state | metre | 14,553
-
Bulgaria | 1866 | state | 4 ft 81/2 | 3,584
-
Burma | 1877 | state | metre | 2,400
-
Canada | 1836 | state | 4 ft 81/2 | 35,147 | private | 4 ft 81/2 | 29,321
-
Ceylon (Sri Lanka) | 1865 | state | 5 ft 6 in. | 1,236
-
Chile | 1851 | state | metre | 3,844 | 5 ft 6 in. | 2,349
-
China | 1881 | state | 4 ft 81/2 | 23,900
-
Czechoslovakia | 1839 | state | 4 ft | 81/2 | 13,226
-
Denmark | 1847 | state | 4 ft 81/2 | 3,395
-
East Africa (Kenya, Uganda. Tanzania) | 1897 | state | metre | 4,370
-
Egypt | 1854 | state | 4 ft 81/2 | 4,149
-
Finland | 1862 | state | 5 ft | 5,462
-
France | 1828 | state | 4 ft 81/2 | 49,028
-
Germany (East) | 1835 | state | 4 ft 81/2 | 18,179
-
Germany (West) | 1835 | state | 4 ft 81/2 | 44,999
-
Greece | 1869 | state | 4 ft 81/2 | 2,002
-
Hungary | 1846 | state | 4 ft 81/2 | 8,442
-
India | 1853 | state | 5 ft 6 in. | 36,353 | metre | 21,770 | 2 ft 6 in.
| 3,513
-
Indonesia | 1864 | state | 3 ft 6 in. | 4,852
-
Iran | 1917 | state | 4 ft 81/2 | 2,5 81
-
Ireland | 1834 | state | 5 ft 3 in. | 2,282
-
Italy | 1839 | state | 4 ft 81/2 | 20,649
-
Japan | 1872 | state | 3 ft 6 in. | 25,426 | private | 3 ft 6 in. | 5,733
-
Korea (South) | 1899 | state | 4 ft 81/2 | 3,378
-
Malaysia | 1885 | state | metre | 1,428
-
Mexico | 1850 | state | 4 ft 81/2 | 30,613
-
Morocco | 1911 | state | 4 ft 81/2 | 1,632
-
Mozambique | 1886 | state | 3 ft 6 in. | 2,551
-
The Netherlands | 1839 | state | 4 ft 81/2 | 4,568
-
New Zealand | 1863 | state | 3 ft 6 in. | 4,499
-
Nigeria | 1901 | state | 3 ft 6 in. | 2,680
-
Norway | 1854 | state | 4 ft 81/2 | 3,452
-
Pakistan | 1861 | state | 5 ft 6 in. | 7,664
-
Poland | 1845 | state | 4 ft 81/2 | 16,540
-
Portugal | 1856 | state | 5 ft 6 in. | 2,944
-
Rhodesia | 1897 | state | 3 ft 6 in.| 2,040
-
Romania | 1869 | state | 4 ft 81/2 | 6,838
-
South Africa | 1860 | state | 3 ft 6 in. | 19,648
-
Spain | 1848 | state | 5 ft 6 in. | 13,792
-
The Sudan | 1900 | state | 3 ft 6 in. | 3,379
-
Sweden | 1856 | state | 4 ft 81/2 | 11,611
-
Switzerland | 1844 | state | 4 ft 81/2 | 4,249 | private | 1,529 | metre
-
Taiwan | 1891 | state | 3 ft 6 in. | 1,061
-
Thailand | 1893 | state | metre | 2,733
-
Tunisia | 1876 | state | metre | 1,743
-
Turkey | 1856 | state | 4 ft 81/2 | 5,874
-
Soviet Union (former) | 1837 | state | 5 ft | 86,691
-
United Kingdom | 1825 | state | 4 ft 81/2 | 34,471
-
United States | 1830 | private | 4 ft 81/2 | 305,179
-
Yugoslavia (former) | 1846 | state | 4 ft 81/2 | 9,433
-
Zaire | 1911 | 3 ft 6 in. | 3,702
-
Zambia | 1905 | state | 3 ft 6 in. | 1,000
-
Predominant ownership is given; most countries have both private and state
owned lines. Gauge of the principal mileage; most countries have lines
of several gauges. So-called "Standard Gauge" = 4 ft 81/2
in.;
"metre" = 3 ft 3 in. Data for early 1970s.
-
Source: Jane's World Railways 1971-1972
|
Units of Measure
 he
premise of the historical review set forth above is that 4 feet, 8.5 inches
is "an exceedingly odd number," by which, no doubt, is meant, "not an integral
number." To be sure, 4 feet, 8.5 inches amounts to 4.70833 feet. he
premise of the historical review set forth above is that 4 feet, 8.5 inches
is "an exceedingly odd number," by which, no doubt, is meant, "not an integral
number." To be sure, 4 feet, 8.5 inches amounts to 4.70833 feet.
-
A track gauge of, say, 5 feet 'even' would probably not be
regarded by most people as an exceedingly odd number.
-
Likewise, lopping off a half-inch gives you 56 inches, which
might not be considered 'odd' in any sense of the word.
| Now, 4 feet, 8.5 inches happens to be exactly 113 on
the 'plug-tine separation scale.'
If you have any doubt of that, pull an electrical plug
out of the wall and take it to the nearest railroad track.
-
Thing is, railroads came first.
|
-

|
If the history of technology has taught us anything, it is
that having standards is a whole lot better than not having standards.
In fact, without standards, the commercial benefits of 'interoperability'
may not be realizable. Interoperability -- like plugs in sockets, like
software in computers, like trains on tracks. Then, too, de facto
standards have a habit of becoming
de jur standards. {Historical
Note}
So, let us not sneer at an emergent standard based on...
-
the war horse's ,
-
the wheel spacing for chariots,
-
the ruts in roads, and
-
the jigs for wagons that were used in the construction of
early railway rolling stock.
If that standard does not comport with our units of measure,
then the latter needs to be replaced. Let us celebrate the achievement
of standardized wheel spacing with a new unit of measure: Metrum
Asinorum (from the Latin for "ass's
measure").
 s
a new international unit, Metrum Asinorum will
unabashedly honor its equine origin along with the wisdom of our progenitors
in the field of transportation technology. Thus, the gauge of railroad
tracks will be forever known to measure exactly 1 metrum asinorum. Who
will deny that as being preferable to 4 feet, 8.5 inches? {Satirical
Comment} s
a new international unit, Metrum Asinorum will
unabashedly honor its equine origin along with the wisdom of our progenitors
in the field of transportation technology. Thus, the gauge of railroad
tracks will be forever known to measure exactly 1 metrum asinorum. Who
will deny that as being preferable to 4 feet, 8.5 inches? {Satirical
Comment}
Application of this new unit outside railroading, though,
will call for some adjustments.
-
Doorways in our homes will be 1.381 by 0.531 metra asinora.
-
What we know as a mile will become 1,121.416 metra asinora
(1.121 kma, perhaps).
-
The length of a football field is 63.717 metra asinora.
We will have to get used to hearing "first and 6.3717 at
the 12.7434 metrum asinorum line," but the sophisticated reader does not
need to be given the whole 5.735 ma.
Metrum asinorum will never enjoy an official sanction
without an Act of Congress, by one of which in July 1, 1901 was set up
the National Bureau of Standards (since 1988 the National Institute of
Standards and Technology -- hmm, it must have been a matter of morale:
Anybody would rather work for an institute than a bureau).
Some, no doubt, will protest that the modern 'meter,'
which is based on physical phenomenon ought to take precedence over the
metrum asinomum. Indeed, the metric system has been modernized to take
into account 20th-century technological advances. But, hey, that was in
1960, long after railroads had reached their zenith. And talk about
"exceedingly odd numbers"! You will see the reason for that exclamation
point in the next sentence, which also ends with an exclamation point:
The meter is now defined as 1,650,763.73 wavelengths
in vacuum of the orange-red line in the spectrum of krypton-86!
Persons concerned about "exceedingly odd numbers" need to
be told that fact -- and a whole lot of other things, including...
What we call a "second" is now defined as the
duration of 9,192,631,770 cycles of the radiation associated with a specified
transition, or change in energy level, of the cesium atom.
But there's something else that my researches turned up.
It really kicks metrum asinorum in the . Read
on.
 he
lampoon of military specifications demonstrated an exceedingly Anglo-centric
view of railroading ("that's the way they built them in England, and the
US railroads were built by English expatriates"). It turns out that only
about 60% of the track-miles of the world have gauges measured at unity
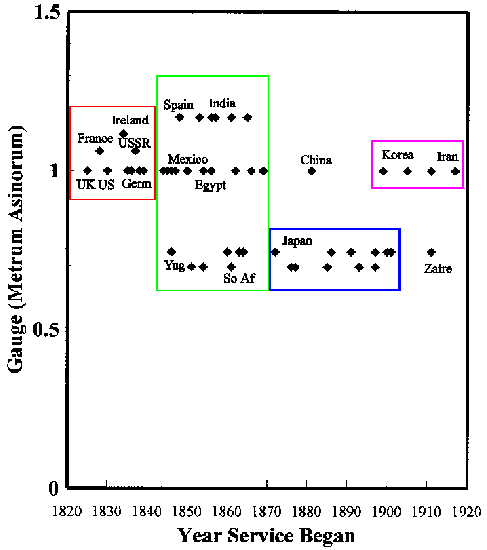
metrum asinorum. Take a look at the adjacent graph. he
lampoon of military specifications demonstrated an exceedingly Anglo-centric
view of railroading ("that's the way they built them in England, and the
US railroads were built by English expatriates"). It turns out that only
about 60% of the track-miles of the world have gauges measured at unity
metrum asinorum. Take a look at the adjacent graph.
Now, based on economic factors, it will be easily argued
that, if one were to select a different gauge, narrower is better (shorter
ties and less ballast, smaller tunnels and bridges). On the other hand,
higher speeds might justify a wider gauge. {Mathematical
Analysis}
As indicated, there are three ranges of track gauges that
have been adopted by the dominant railroads (usually state owned) in various
countries around the world. In addition to 1.0 ma, adopted by 29 railroads,
there are 19 countries that have tracks separated by about 0.7 ma and 9
railroads built with approximately 1.15 ma between rails.
-
The wider gauges are curiously close to what Europeans have
adopted as a standard for their building trades ("one meter eighty") --
possibly a mere coincidence.
-
In round numbers, the narrow gauges are clustered at about
1 meter (1,650,763.73 wavelengths in vacuum of the orange-red line of the
spectrum of krypton-86) -- definitely not a mere coincidence.
Which raises the subject of decision-making throughout the
history of railroads, as depicted in the following scattergram:
...from which it is possible to discern four
eras characterized solely by the selection of track gauges...
|
1820-1840
|
Domination by
G = 1.0 Standard
|
Notice how France is in there between Britain and the
United States at 1.5 meters (1.062 ma); Ireland comes along at 1.6 meters;
later on, the countries that would become the USSR adopted the French standard;
all the rest in this era (Germany, Belgium, Canada, Austria) go along with
the British standard. |
|
1840-1865
|
Three Standards
Emerge
|
Six national railroads go wide, seven go narrow, and
ten adopt G = 1.0 ma. Perhaps this was a time of wild experimentation.
Preferences seem not to have been correlated to continents. |
|
1865-1900
|
Domination by
Narrow Gauge
|
Only one country opted for G = 1.0 (China) during this
period; nine went for variations of the 1 meter standard. |
|
1900-1920
|
Return of the
G = 1.0 Standard
|
During the 20th century, only one out of five nations
put a narrow gauge railroad into service (Zaire -- now, Congo). |
Enough said. Well, almost
enough said...
As mentioned above, there are economic benefits to be
derived from building tracks with gauges smaller than 1 ma; nevertheless,
the Bay Area Rapid Transit (BART) system, which was put into service in
1972, has a track gauge of 1.189 ma (oh all right, 5 feet, 6 inches). Ever
curious, I asked a BART engineer why they chose that track gauge.
"To fit the cars," he answered, wiping a smirk from his
face.

Stand
and Deliver
The tone of this analysis reminds me of an anecdote told
by Antony Jay in Management and Machiavelli. Following a routine
exercise of a British artillary unit during WWII, Antony Jay inquired of
the field commander why one of the soldiers stood at attention throughout
the maneuver.
"He's number six," replied the General.
"I can count, sir. But what is number six supposed to
do?"
"That's his assignment. Number six stands at attention."
"While all the others run around positioning the cannon,
loading, and firing?"
"Yes, of course," grunted the General. "It's always been
that way."
Sure enough, when Antony Jay followed up by examining the
official military documents, he came upon the reason: "Number six," said
the manual, "holds the horses." {Return}
Royal
Cubit
The royal cubit was developed about 3000 BC based on the
length of the arm from the elbow to the extended fingertips. Not precise
enough for you? The ancient Egyptian standardized the measurement by a
royal master cubit of black granite, against which all the cubit sticks
were measured at regular intervals. Some will complain that the royal cubit
(524 millimetres or 20.62 inches) was subdivided in an complicated way...
The basic subunit was the digit (width of a finger,
don't you suppose?). There were 28 digits in the royal cubit. Naturally,
four digits equaled a palm, five a hand. Twelve digits, or three palms,
equaled a small span. Fourteen digits, or one-half a cubit, equaled a large
span. Sixteen digits, or four palms, made one t'ser. Twenty-four digits,
or six palms, were a small cubit. Tell your friends.
The digit was in turn subdivided. The 14th digit on a
cubit stick was marked off into 16 equal parts. The next digit was divided
into 15 parts, and so on, to the 28th digit, which was divided into 2 equal
parts. Thus, measurement could be made to digit fractions with any denominator
from 2 through 16. The smallest division, 1/16th of a digit, was equal
to 1/448th part of a royal cubit.
The accuracy of the cubit stick is attested by the dimensions
of the Great Pyramid of Giza. Although thousands were employed in
its building, its sides vary no more than 0.05 percent from the mean length
of 230.364 metres (9,069.45 inches).
One cannot talk about civilized history without mentioning
the Magna Carta (1215), which contains a clause to correct measurements
applicable to grain and, most importantly, wine. A standard yard, "the
Iron Yard of our Lord the King," was prescribed for the realm, divided
into the traditional 3 feet, each of 12 inches, "neither more nor less."
The perch (later the rod) was defined as 5.5 yards, or 16.5 feet. The inch
was subdivided into 3 barley corns, which means that the so-called standard
railroad gauge of today can really be explained by its equivalance in barley
corns (168). {Return}
Show Respect
In olden times, people snickered at one definition of
a "horse show"...
A bunch of horses showing their es
to a bunch of horse's es showing their horses.
...which, of course, disparaged the owners of the horses
not the owners of the horse's es. {Return}
Track
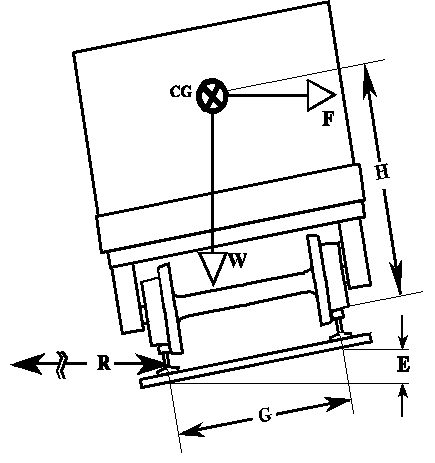
Gauge and Train Speed
Trains are typically much wider than the tracks on which
they run, so volumetric efficiency must play a minor role in the decision
process. Stability, though, is another matter.
The wider the track gauge, the faster a train can operate
without falling over when going around a curve. The maximum speed can be
increased for any given track gauge, of course, by elevating the outside
rail relative to the inside rail ('super-elevation' is the term of art).
The limiting factor is center of gravity. Generally speaking, the greater
the payload, the higher the center of gravity. For every vehicle in the
'consist,' the location of the center of gravity above the rails must be
taken into consideration in two ways...
-
At high speed a high center of gravity subjects the vehicle
to an outward roll-over for a given super elevation.
-
At low speed -- hey, like stopped -- a high center of gravity
subjects the vehicle to an inward roll-over for a given super elevation.
Much attention has been given to 'tilt technology' (the Pendolino,
in Italy), which embeds a tilting mechanism in the suspension of each railway
coach -- a synthetic form of super elevation, one might suppose. Not so.
The purpose is to provide passenger comfort more than stability.
For sophisticated readers who are inclined to recreational
calculations, it is possible to estimate the effect of track gauge on maximum
allowable train speed, ceteris paribus. You will observe that in
the vicinity of G = 1.0 metrum asinorum, a change in track gauge of as
much as 30% will produce a change in maximum train speed of only 10%. This
assumes a level track and all other variables held constant. The following
expressions were derived using First Principles, assuming an exact balance
between weight and centrifugal moments:
| VMAX = sqrt ((R * g * (H * sin (B) + (G / 2) * cos (B)) / (H
* cos (B) + (G / 2) * sin (B)));
Eo = G * sin (arc tan (((Vo ^ 2) - G / (2 * H)) / (1 -
((Vo ^ 2) * G /(2 * H))))
where...
-
VMAX = maximum train speed (fps)
-
Vo = VMAX @ G = Go
-
G = track gauge (ft)
-
Go = 1 metrum asinorum (4 ft, 8.5 in)
-
E = super elevation of outside rail (ft)
-
Eo = super elevation to achieve Vo
-
g = gravitational acceleration (fpsp)
-
R = radius of track curvature (ft)
-
H = height of center of gravity (ft)
-
B = bank angle (rad); B = arc sin (E / G), where...
-
F = centrifugal force (lb);
-
F = (W / g) * (VMAX ^ 2)) / R, where...
W = vehicle weight (lb)
|
 |
It may be interesting to note that a track gauge of G = 0.5
metrum asinorum (the temptation to say "half-assed" is irresistible) would
impact maximum train speed by only about 30%, and this can be easily overcome
by super-elevation of the outside rail...
Consider a segment of level track with a gauge
of 1 metrum asinorum has a radius of curvature of 1,250 feet. A vehicle
with its center of gravity located 15 feet above the track, would be able
to operate on that curve at up to 54 mph without tipping over. If the track
gauge were cut in half, the maximum speed would be reduced by approximately
30% to 37.8 mph. Now, by elevating the outside rail only 2.25 inches, the
train could operate again at 54 mph.
The previous sentence might warrant an exclamation point.
{Return} |