Ellipse Illusion

Copyright ©2015 by Paul Niquette. All rights reserved.
 

American inventor Charles Kettering famously asked, “Why is grass green?”  The explanation he received from experts: Leaves of grass have chlorophyll in them, and chlorophyll is green.

The question "Can you explain why that conic section is not an oval?" was posed to all of the consultants@niquette.com and received technical assurances that slicing a cone does indeed produce an ellipse (see Epilog).  Only one respondent attempted to explain the Ellipse Illusion...

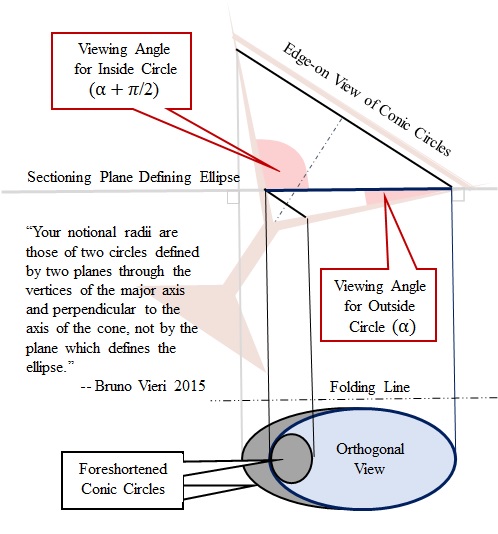Conic Tonic

The sketch draws attention to [deep breath here] the compensating curvature resulting from differences in foreshortening of the osculating circles ("notional radii" in the text above) at opposite ends of the closed curve inscribed upon the sectioning plane by the surface of the cone.  For our solution, let us reprise and correct my fallacious explanation for the Ellipse Illusion...

The local radius of curvature for a smooth shape is defined by the radius of the osculating circle at each point, such that one end of the oval vertex of the ellipse drawn upon the sectioning plane seems to share fits the obliquely foreshortened osculating circle of the cone at a point near its apex where the radius is small while the opposite end of the oval vertex of the ellipse drawn upon the same sectioning plane seems to share fits the acutely foreshortened osculating circle of the cone at a point farther away from its apex where the radius is larger.

Orbits are ellipses.  Every ellipse is symmetrical about both its major and minor axes.  An ellipse has two foci.  Only one focus is occupied by a celestial body with the gravitational mass that maintains the orbit.  Anything going on at the other focus?  My intuition wants to know.

Line

Acknowledgements

Permit me to offer an appreciative toast to Rich Alexander, Jürgen Köller, Ed Moore, John Swanson, Bruno Vieri, Leonard Zane for their contributions to the solution page of the Ellipse Illusion...
Martini
 

Home Page
Puzzle Page
Space Stuff
The Puzzle as a Literary Genre
 
 

Epilog:

The Ellipse as a Conic Section
-- Leonard Zane 2015

An ellipse is the boundary formed by the intersection of a plane with a cone.  The example below shows how the center of the ellipse is NOT the same as the center of the cone.

The general equation for a cone that is symmetric about the +z-axis is,

z = A (x2 + y2)1/2 and for simplicity set A = 1

The equation for a general plane is,

a x + b y + c z = 1

Again to simplify the analysis, consider only planes parallel to the x-axis.  These planes intersect the y-z plane in straight lines,

z = my + b and set the z-intercept b = 1

In order for the plane to cut completely across the cone,

m < |1|  -->  and for this example m = ½  -->  z = ½ y + 1

The equation for the intersection of the cone with this plane is found by eliminating z between the two equations.

½ y + 1 = (x2 + y2)½  -->   ¼ y2 + y + 1 = x2 + y2 -->  1 = x2 + ¾ (y2– 4/3 y)

Complete the square to get,

1 = x2 + ¾ (y – 2/3)2 – 1/3  -->  4/3 = x2 +3/4 (y – 2/3)2

Re-arranging terms to put into the canonical form for an ellipse symmetric about the x and y-axes,

1 = x2 / (4/3)2 + (y – 2/3)2 / (16/9)2

This is the equation for an ellipse with a center at x = 0 and y = 2/3 with a minor axis of 8/3 and a major axis of 32/9.