|
Copyright ©2010 by Paul Niquette. All rights reserved. |
|||
A simple formula for distance is x = a t 2 / 2 and if we substitute that same value for acceleration, x = (108.4 ft/sec/sec)(4.45 sec)2/ 2 = 1,074 ft -- not 1,320 ft...BLAGH We have found that with an acceleration of 3.37 g, the car reaches 329 mph at a point 246 feet before reaching one quarter of a mile and would thus be traveling faster than 329 mph when it reaches the finish line. How much faster, we wonder? By rearrangement of a = v / t to read t = v / a then substituting that into x = a t 2 / 2 and solving for v = [2 a x ]1/2, we get v = [2 (108.4 ft/sec/sec)(1,320 ft)]1/2 = 534.9 ft/sec = 364.7 mph upon reaching the finish line -- not 329 mph...BLAGH Turning that formula around, we can write a = 2 x / t 2 and for x = 1,320 ft and t = 4.45 sec, we calculate that a = 2 (1,320 ft) / (4.45 sec)2 = 133.3 ft/sec/sec = 4.14 g, which matches Choice {2}; however... Going back to our first formula and turning it around, we write v = a t, such that for a = 133.3 ft/sec/sec and t = 4.45 sec, we get speed: v = 593.2 ft/sec = 404.5 mph at the elapsed-time target, 4.45 sec -- not 329 mph...BLAGH
The diagram on
the right depicts two different acceleration
models. In red is a Ramp-Down profile. It starts the
quarter-mile run at a peak value of acceleration a
= 5.68 g and ramps linearly down to 0.93 g at the
finish line. Sure enough the dragster
completes the run in 4.45 seconds traveling 329 mph,
which matches Choice {3} and solving the World's Fastest Dragster puzzle...
However, there is just this one other consideration. An acceleration of 5.68 g at the beginning of the run places a ferocious demand on traction. Whatever its horspower, the dragster's tires must deliver a force that is 5.68 times the weight of the car -- all without the benefits of aerodynamic down-force! Exclamation point deserved. Depicted above in blue is a Step-Down profile. It starts the quarter-mile run at a peak value of acceleration of only 4.15 g (for large values of "only"). At a point about 1,000 feet into the run (3.43 seconds), the acceleration is reduced to 0.42 g. Of course there would be no incentive to do that. Our solitary purpose in doing so is to solve the puzzle. Indeed, if that acceleration of 4.15 g could be maintained for another second, a new world record of 4.44 sec for the quarter mile would be set. A mere 100th of a second might not seem like much, but in a side-by-side run, the fans in the stands would be able to confirm the win with alacrity. There are
doubtless other models for dragster accelerations,
and you are invited to send them here. Epilog:
In 2017, David Walker wrote, "Another closely-related question is,
'What horsepower is required to produce this
record-setting result?' The short answer is, something
north of 5,000 hp. One wonders how that is possible in
a motor that's usually designed for sustained output
of maybe 1,000 hp max. The answer lies in the
thermodynamics more so than the mechanics. That is,
eliminating the excess heat that cannot even anywhere
closely be dissipated outside of the mass of the
engine in a five-second run.
|
 An
elementary analysis might begin with this simple
formula a = v / t.
An
elementary analysis might begin with this simple
formula a = v / t. 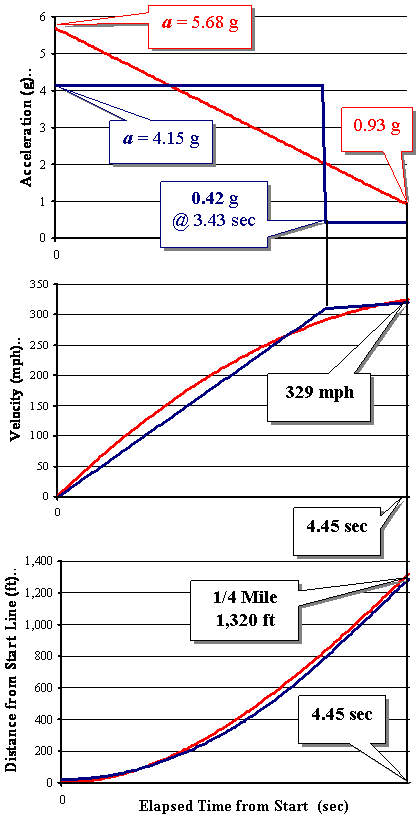 Sophisticated solvers
will have observed from the outset that our analysis
so far is based on an
Sophisticated solvers
will have observed from the outset that our analysis
so far is based on an