 |
|
Copyright ©2014 by Paul Niquette. All rights reserved. |
|
| Terminal
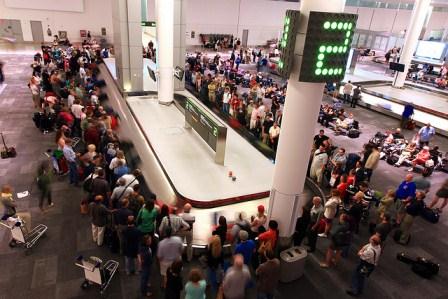
Operations Isn’t that a mighty ominous name for a department? Hey, at an airline company? Still, every airline must have a business unit responsible for baggage services: check-in and loading prior to departures, unloading and baggage claim upon arrival. In the early ‘60s the ‘jet age’ was just – well, taking off. Less than a quarter of Americans had ever flown. Speed was in the air – but not only in the air. Time was of the essence on the ground as well. Flying at 500 mph was an exciting new experience for millions. But what’s the point, if it takes an hour for checking in and another hour for baggage claim?  hough hardly as glamorous
as flying, Terminal Operations are nevertheless
necessary. And
costly. Capital
equipment for handling baggage calls for immense
investments, and most functions are labor intensive as
well. For
performance, the most demanding challenge is to
provide prompt delivery of every piece of baggage to
its owner after arrival.
Even with on-time departure and arrival, the
time spent waiting for luggage is perceived by
passengers as directly added to the duration of the
flight. Following arrival of each flight, there is a time required for passengers to flow out of the aircraft and make their way through the terminal to Baggage Claim. Processing of baggage might be completed concurrently with that interval. However that presumes a full complement of equipment and people-power idly standing by for instant deployment even as the airplane’s wheels are being chocked. Meanwhile, what about the earliest passengers out the door? They will surely be called upon to endure some amount of lingering after they get to Baggage Claim. How much waiting time will be tolerated? Fifty years ago, that was the key question for Terminal Operations.Grand Experiment If asked, all passengers would say they want their luggage to be waiting for them in Baggage Claim with zero waiting time. Best not ask. A certain major airline had a statistician on staff in Terminal Operations who proposed a Grand Experiment. The objective was to ascertain a realistic estimate for the time available after arrival of a typical aircraft for unloading and distributing baggage to passengers. A statistical measurement of customer tolerance was needed. Here is how the Grand Experiment worked.  t airports, on selected
flights, the Terminal Operations staff arranged to
have all baggage secretly withheld from the
arriving passengers.
Solvers may want to reread the previous
sentence. Luggage
was withheld, that is, until there was an inquiry by
one of the passengers.
Guided by the Terminal Operations staff at
headquarters, the airline enlisted shift supervisors
at each terminal to make clandestine measurements of
the interval between when the plane
arrived at the gate and the first passenger inquiry
was received by an airline employee. Baggage and
suitcases would then be released, thence allowed to
flow along conveyers and to slide onto the carousels
to be claimed.
 Solver might be reminded that the Projected Distribution depicts the frequency of time intervals to first complaint among various flights, not some other distribution of complaints among passengers. The instant the first complaint was recorded, the experiment for that flight was over. hus, one sees that the hypothesis
included 45 minutes for the average time to first
complaint. Some
flights would have shorter than average intervals,
others longer than average. Various factors were
considered to be relevant to those deviations.
Solvers are here given the opportunity to see a
representation of the Actual
Distribution from data produced by the Grand
Experiment… Hmm. The Actual Distribution turned out to be “bimodal”! Solvers will observe the exclamatory punctuation at the end of the previous sentence and this one!
That all came as a complete surprise to the statistician in Terminal Operations. It was good news, though. The indicated shift would surely grant extra time for baggage delivery. But its cause was something of a mystery... What is your explanation? 1. Length of Flight................................... Longer vs Shorter
|
