Historic Car Crash

Copyright ©2011 by Paul Niquette All rights reserved.

Featured in the Historic Car Crash puzzle is a photograph taken by a Speed Graphic camera like this one, which dates back to the 1930s.  Look closely and you will see a solenoid mounted horizontally below the lens.  It was designed to be activated by a speedgun unit for synchronizing the shutter with a flash attachment (not shown in the photograph). 

For the car-crash photograph, the solenoid was activated by an electronic timer, which was built in the laboratory of ITTE.  The design of that timing device is quite a story in itself, inasmuch as transistors, let alone microprocessors, were not commercially available in 1954. 

An interested solver might like to try his or her hand in the design of a monostable, one-shot multivibrator using a pair of vacuum tube triodes.

A little parsing music, please: Notice that the Historic Car Crash puzzle does not seek a prediction of collision forces and energy dissipation.  ITTE's research, of course, would give paramount importance to those topics, but the puzzle merely calls for a time interval.  According to Engineered Automobile Crashes a timer tripped the shutter at a precise interval after the car contacted the barrier in order to capture the instant of "maximum deceleration and crush-in volume."  That phraseology, by the way, was specified by Derwyn Severy, the project engineer.  Both of those measurements might pertain to the car itself.  But what about the second impact and the collision forces that cause injuries to people?

For the Historic Car Crash puzzle, let us reprise the 1954 analysis by the research assistant...  

He began by noting that the time of maximum deceleration Tmax-decel experienced by the anthropometric dummies would necessarily take place after the time of maximum crush-in volume Tmax-crush for the vehicle, thus Tmax-decel > Tmax-crush. 
Conservation of the vehicle's kinetic energy seemed like a macrocosmic way to estimating Tmax-crush, but it led into a blind alley.  With the weight of the vehicle W and speed V both known, the kinetic energy at impact was given by (1/2)(W/g) V2.  That energy would have to be dissipated as heat and sound in the crunching of the vehicle frame by an unknown force Fmax-crush multiplied by Xmax-crush (see Observation #1) -- plus the lifting of the vehicle's center of mass by some Ymax-crush (see Observation #2) along with whatever energy gets absorbed in the barrier and the planet earth.  All those variables, even if perfectly known, were useless in estimating an amount of time -- Tmax-crush.
A microcosmic analysis began with a conventional equation that relates stopping distance and stopping time: Tmax-crush = 2 Xmax-crush / V.  With V = 28 mph = 41 fps and Xmax-crush = 2.5 ft, the result was Tmax-crush = 0.061 seconds = 61 milliseconds.  A cursory review of the film from the first crash test, even with frames separated by 25 ms, indicated that this time was too short.  No wonder.  The calculation made a hidden assumption: constant deceleration.
A more realistic model for the crash applied an elastic assumption for the vehicle frame ("elastic" up to a point -- the yield point of the materials in the structure).  A metal, in particular steel, acts pretty much like a spring, resisting stress in proportion to strain until reaching its elastic limit.  Stress or force (f) during a collision starts out at zero and increases with crush-in displacement (x) linearly (f = k x) until reaching some maximum, such that f = Fmax-crush and x = Xmax-crush, after which f drops to zero and x stays equal to Xmax-crush. 
The deceleration of the vehicle is given by d2x/dt2  = - (k / m) x  (Newton's Second Law), where m represents the mass of the vehicle (m = W / g) and the minus sign indicates that the collision force resists the inertia of the vehicle, which will hardly surprise anybody. 

Sophisticated solvers will recognize the equation d2x/dt2  = - (k / m) x as the most familiar homogeneous second-order linear, constant coefficient ordinary differential equation, which is best known for its power to describe simple harmonic motion (animation).

The research assistant's mathematical model, in effect, had a 1937 Plymouth 'vibrating' linearly back and forth in obedience to x = Xmax-crush cos[(k / m)1/2 t], such that the period is given by the following expression: 2 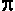 / ( k / m)1/2.  Well, of course, the vibration ceased after only one-quarter of its period, with x = Xmax-crush, as the car's structure stopped its "harmonic motion."  Accordingly, Tmax-crush = (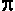 / 2)  (m / k)1/2.

Here may be a surprise for some people: Tmax-crush is independent of Xmax-crush and therefore independent of the speed of the vehicle V!  The exclamation point would have been an undeserved indulgence at this point in the analysis, inasmuch as the research assistant did not yet have an estimate for Tmax-crush.  Whatever that turns out to be, though, it will be almost constant for a range of crashing speeds and vehicle damage characterized by Xmax-crush. 

Back in 1954... 

Finding the value of m / k required three more assumptions... 

[1] That the values of both m and k are constant over the range 0 < x < Xmax-crush. 
[2] That 100% of the kinetic energy of the vehicle is absorbed by the vehicle.
[3] That an average Fmax-crush) / 2 prevails throughout the range 0 < x < Xmax-crush. 
As noted above the vehicle's kinetic energy is given by (1/2)(W/g) V2.  Based on the assumptions, k = (W/g) (V/ Xmax-crush)2 and Tmax-crush = (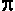 / 2) (Xmax-crush / V).  Accordingly, for Xmax-crush = 2.5 ft and V = 41 fps, Tmax-crush = 96 milliseconds.

Now, with respect to the second impact and the fact that Tmax-decel > Tmax-crush,  ITTE's research focussed on the right front seat, which in those days was commonly called "the death seat." That funereal phrase gave recognition to the vulnerability of passengers seated thereon.  A post-crash photograph in the article showed one hapless anthropometric dummy that suffered horrendous consequences that day while riding in the death seat.  Let us continue with a review of the 1954 analysis by ITTE's research assistant...

An unrestrained passenger in the right front seat would still be moving forward at 28 mph = 41 fps while the vehicle abruptly stops.  The separation between the passenger's head and the nearest structure inside the car (ceiling, windshield, dashboard) might be two feet.  That distance would be covered in about 50 ms, which implied a shutter interval based on Tmax-decel = 96 + 50 = 146 ms.   But there was more to consider.
The anthropometric dummies had "joints with movement and fixation closely resembling that of a person forewarned of an impending collision."  With forewarning before the first impact, a typical front-seat passenger ought to be able to double that 50-ms delay, thereby deferring his or her second impact  to about 200 ms after the car contacts the barrier. That was the argument made by the research assistant to the project engineer. 

And the rest is history.  Thus, the solution to the Historic Car Crash puzzle can be... 

The high-resolution picture should be snapped 200 milliseconds after the car contacts the barrier.


Epilog: 

More than a half-century later, sophisticated solvers will surely want to reconsider -- all right, second-guess -- the three assumptions above... 

[1] Values of m and k are surely not constant over the range 0 < x < Xmax-crush.  Inasmuch as the harmonic period and therefore Tmax-crush is proportional to (m / k)1/2, one must expect that...

  • Tmax-crush will decrease with m, as more and more parts of the vehicle -- especially the engine -- become stopped against the barrier. 
  • Tmax-crush will increase as k weakens during the crash with metals yielding and fewer parts of the structure participating in the 'stiffness' of the 'spring'. 
    • Thus these two effects seem to offset each other, and thus did think ITTE's research assistant.

    [2] Of course, something less than 100% of the kinetic energy of the vehicle was absorbed by deformation of that old Plymouth.  For one thing, the back end was lifted up in an obvious partial conversion of kinetic to potential energy.  Most likely, Ymax-crush acts in reciprocity with Xmax-crush, but it is hardly clear, even today, what effect energy shifts would have on Tmax-crush.

    [3] Sophisticated solvers of the Historic Car Crash puzzle undoubtedly doubt that a perfectly linear average (f =Fmax-crush / 2) would prevail throughout the range,  0 < x < Xmax-crush.  Today, with a simple spreadsheet, people can lash up a piece-wise model to explore non-linear elasticities for a crashing automobile.  However, many will be astonished to see how little Tmax-crush changes with various shaped curves postulated for k-versus-x. 
     
     


    Home Page
    Puzzle Page
    Math and Models
    The Puzzle as a Literary Genre