Band Around the Earth

he diagram shows that the length of the original band can be calculated by multiplying the diameter of the earth (assumed to be approximately 8,000 miles) by

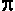= 3.14159265359.

The new circumference can then be calculated by merely adding 10 feet, as specified in the puzzle.

The solution to the puzzle comes down to calculating the diameter of a circle with a circumference equal to the lengthened band, which will be larger than the diameter of the earth by some unknown amount x. The sophisticated puzzle solver will immediately see an opportunity to write an equation...

(8,000 miles) 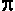+ 10 feet = (8,000 miles + x)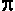
Which can be solved for the unknown x...

x = 10 feet / 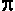= 3.183 feet

...half of which (1.59 feet = 1 foot 7 inches) represents the gap between the lengthened band and the surface of the earth.

That may be large enough for a rather slender person to crawl under.

oo-ha! That's the sound of a sophisticated puzzle solver making a discovery. In this case, he or she will observe that the diameter of the earth does not matter at all -- that the gap would be the same (1 foot 7 inches) whether the band were wrapped around the moon or a basketball or a marble.

The solution, in fact, is merely the radius of a circle that has a 10-foot circumference.

Home Page Puzzle Page Math and Models The Puzzle as a Literary Genre