Balls in Boxes

Balls in Boxes

et us suppose that you have by pure chance removed a red ball from either box without seeing inside. In deciding whether to accept the wager, you must first decide which box is more likely to give you a matching red ball ("success" in the parlance of probability theory).

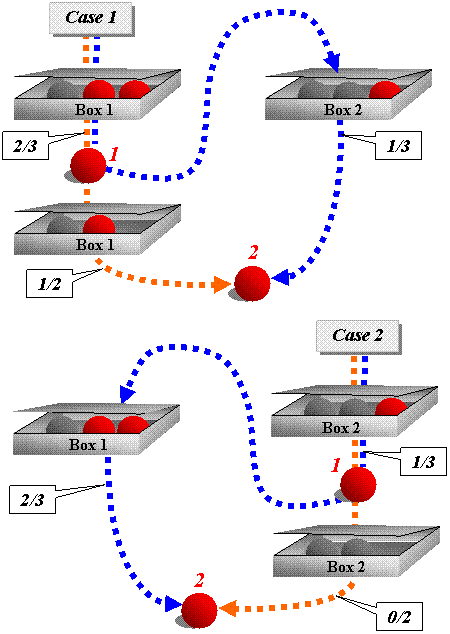On the right is a diagram depicting two cases that will help you make your decision. Both cases have arbitrarily assumed that Box 1 contains two red balls and one black, while Box 2 contains two black balls and one red. Case 1 postulates that the red ball was removed from Box 1, and Case 2 postulates that the red ball was removed from Box 2.

In both cases, the orange path indicates that you have decided to take the second ball from the same box, and the blue path indicates that you have decided to take the second ball from the opposite box.

Pathway links are marked with their respective probabilities. Accordingly, the probability that the first ball would be red is 2/3 in Case 1 and 1/3 in Case 2. Now, the first ball is known to be red, so those particular probabilities really pertain to what is not known, namely the particular arrangement of the Balls in Boxes that is consistent with the indicated probability.

Same Box

In Case 1 the orange path shows a probability of 1/2 that the second ball taken out of the same box will be red. But that's not the whole story. You must take into consideration the probability that the first ball was red, which is 2/3. The joint probability that the second ball will match the first ball (success) is given by the product of their individual probabilities (2/3)(1/2) = 1/3.
In Case 2 the orange path shows a probability of 0/2 -- impossible -- that the second ball taken out of the same box will be red. That would be just about the whole story, since it does not matter what the probability is that the first ball was red (1/3). The joint probability that the second ball will match the first ball (success) is given by the product of their individual probabilities (1/3)(0/2) = 0.

Since Case 1 and Case 2 are equally likely, the overall probability of success if you make your selection from the same box is given by (1/3 + 0) / 2 = 1/6 < 1/2 (less than an even bet).

Opposite Box

In Case 1 you see the joint probability of success on the blue path if you take the second ball out of the opposite box will be given by (2/3)(1/3) = 2/9.
In Case 2 you see the joint probability of success on the blue path if you take the second ball out of the opposite box will be given by (1/3) (2/3) = 2/9.

Again, Case 1 and Case 2 are equally likely, so the overall probability of success if you make your selection from the opposite box is given by (2/9 + 2/9) / 2 = 2/9 < 1/2.

Don't take the wager.

Epilog

Sophisticated solvers may want to investigate variations of the Balls in Boxes puzzle. Here are a few questions that come readily to mind:

What will be the effect of having the boxes start out containing m red balls with n black balls and m black balls with n red balls?
What values of m and n will make an even bet advisable?
Try putting all m plus n balls in one box and take out two at random. What is the probability that they are both the same color?

Meanwhile, a search on the worldwide web using the title of this puzzle turns up more than a thousand sites that deal with such diverse subjects as Network Processes, Quantum Gravity, Wind Damper Design as well as Probability Questions. Tell us about your favorites here.

Home Page Puzzle Page Logic and Reasonings The Puzzle as a Literary Genre