Skateboarding tricks are dominated by jumping.  Stairways are exceptionally challenging obstacles.  Unlike curbs and benches or simple precipices, an outdoor stairway requires the skateboard jumper to cover a long horizontal distance while dropping an immense vertical height. Aaron Homoki's record-setting jump was from a height of 4.5 meters (14 ft 9 in, 7 inches per stair) and over a distance of 6.7 meters (22 ft, 10.6 inches per stair).  Referring to the generalized dimensions in the sketch below: yS and xS represent the height and length of the stairs, while yJ and xJ represent the height and length of Homoki's jump above and beyond the top stair. 

• Let vX represent Homoki’s horizontal velocity as he jumped vertically above the top stair.  As will be observed in the video Jaws vs the Lyon25, that horizontal velocity vX appears to remain constant throughout the jump -- and beyond!  Please note the exclamation point.
• Let vY represent Homoki's instantaneous vertical velocity, which does change throughout the jump under the influence of constant gravitational acceleration g.  Decreasing gradually to zero at the zenith of the trajectory, vY then increases to its maximum, approaching the ground.  Immediately after the board contacts the ground, the vertical velocity, vY suddenly reduces to zero.
  

Solvers are invited to characterize the trajectory of Homoki's jump by elementary physics, whereby the acceleration of gravity g = 9.8 meters/sec/sec (32.2 ft/sec/sec), and m represents the mass of the skater plus that of the skateboard taken together.  For simplicity we shall apply the law of Conservation of Energy, beginning with these relationships...

• kinetic energy = (1/2) mass x total velocity squared
  
• potential energy = weight (m g) x height above ground

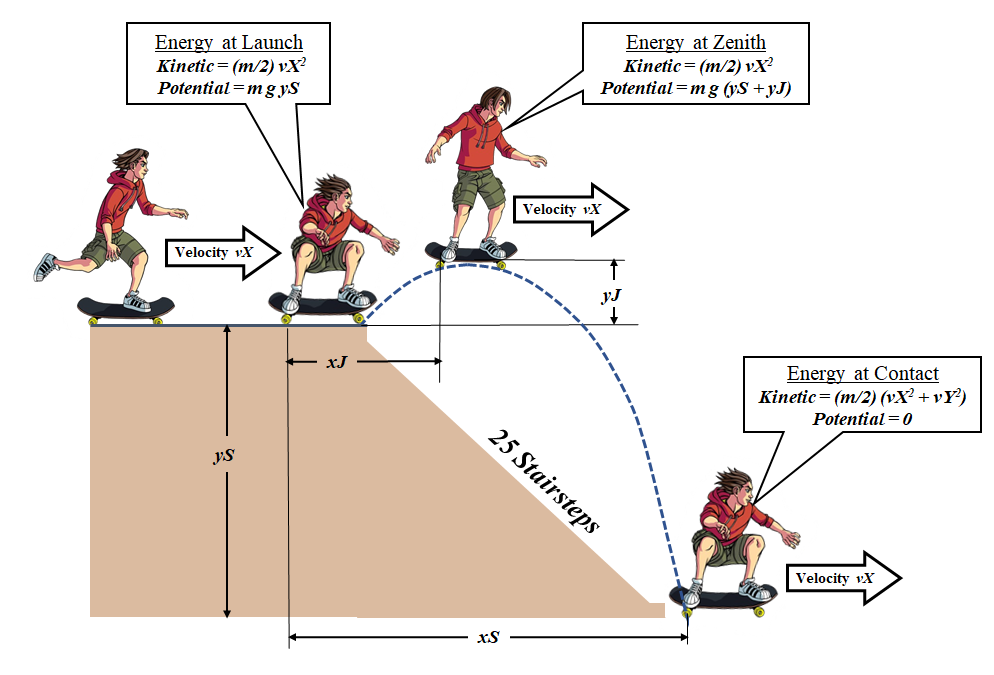
...and since velocities (vX, vY) are vectors, total velocity = (vX^₂ + vY^₂) ^1/2  by the Pythagorean Theorem.

Inasmuch as energy can neither be created nor destroyed, Energy at Zenith = Energy at Contact, and the following equation applies to the skateboard trajectory:

(m/2) vX² + m g (yS + yJ) = (m/2) (vX² +vY²), which can be simplified algebraically to read...
m g (yS + yJ) = (m/2) vY²

Oh, but then, immediately after contact, vY = 0 and thus m g (yS + yJ) = 0.  Hmm.  The potential energy at zenith seems to have suddenly vanished.  Accordingly, here is what one might call the Skateboard Mystery...