Sometimes one door-leaf won't close.  For safety's sake, all the passengers must give up their seats, grab their laptops, and get off the train, thence to stand around waiting on a crowded platform for the next train, which will be due in tH.  Meanwhile, the empty, otherwise healthy 'consist' goes rattling on down the track toward the maintenance shop. 

Propulsion or brake failures are rare, but the time to restore service may result in giving the train a "bad-order."  In worst-case bad-orders, the train cannot be moved.   During commuting rush-hours, that necessitates what is called, without affection, "Single Tracking."

Figure 0a shows Normal Operations and provides definitions for terms that will be used in this puzzle.  Three stations are depicted (A, B, C) along with double-track, right-running trains, eastbound (EB) on Track 1 and westbound (WB) on Track 2.  The time-tables for each direction can be independent of each other.   Stations are separated in pairs by distances xAB and xBC, and for simplicity the respective trip-times are tAB and tBC.  Two interlockings (iA and iC) are aligned for Normal Operations, each interlocking is equipped with double crossovers that enable trains to change tracks if the need arises. 

In Figures 1 and 2, a bad-order train is shown stopped at Station B on Platform 2, in effect taking all of Track 2 out of service between Stations A and C.  In Figure 1a, we see an EB train on Track 1 that is not immediately affected by the bad-order train on Track 2.  A WB train at Station C on Platform 2 will not be able to proceed on Track 2 and must therefore off-load all of its WB passengers, including those who may have just boarded.  At some point, of course, the WB train at Station C should be turned back, perhaps to become an EB train, departing from Platform 2 and crossing over to Track 1 via iC as depicted in Figure 1b.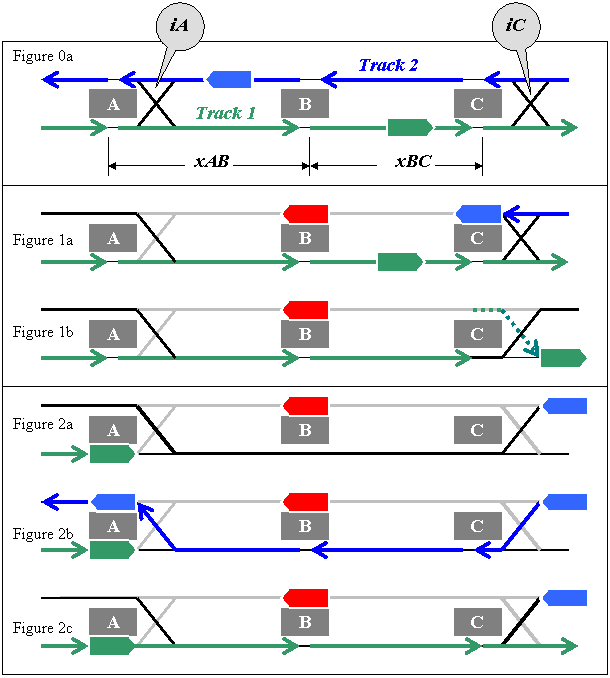

In Figure 2a, we see that Single Tracking is about to commence.  Two trains are in effect competing for the use of Track 1: an EB train at Station A Platform 1 and a WB train approaching iC on Track 2.  Figure 2b shows that priority has apparently been given to the WB train.  The switches in both iA and iC have been aligned to permit the WB train to cross over to Track 1 via iC and provide service for WB passengers at Stations C and B, crossing back to Track 2 via iA to provide WB service to Station A on Platform 2.  For large values of tAB and tBC, the effect of slowing for cross-overs in iA and iC will be negligible.

Figure 2c illustrates how the EB train at Station A will be able to occupy Track 1 immediately after the WB train clears iA.  By inspection, sophisticated solvers will estimate that during Single Tracking the single-tracking headway can be estimated as the round-trip time between interlockings, thus tHSINGLE-TRACKING = 2(tAB + tBC). 

Test Case  Let: tHDOUBLE-TRACKING = 6 minutes, tAB = 7 minutes, tBC = 8 minutes. That means tHSINGLE-TRACKING = 2(7 + 8) = 30 minutes.

A passenger showing up randomly at any of the three stations A, B, C expecting to wait an average of tHDOUBLE-TRACKING / 2 = 3 minutes for the next train, will be disappointed at having to wait around tHSINGLE-TRACKING / 2 = 15 minutes.